What Affects Reconstruction Accuracy?
Upsampling Algorithms, Precision and Noise Shaping
Reconstruction accuracy in the context of upsampling refers to how well the upsampled signal approximates the original (analog) signal. It is a measure of how closely the interpolation process used during upsampling preserves the characteristics and fidelity of the original audio signal. This is crucial for maintaining audio quality and avoiding artifacts.
Reconstruction accuracy depends on the quality of upsampling algorithm and/or filters used, the precision of the calculations, and the application of noise shaping. The choice of upsampling algorithm is critical as it determines how the new samples are generated. The precision of the calculations affects the accuracy of the interpolation process, with higher precision leading to more accurate reconstruction. Noise shaping is used to reduce quantization noise, which can introduce artifacts in the upsampled signal. By shaping the noise, quantization noise it is moved to frequencies where it is less audible, preserving the accuracy of the signal and improving the overall audio quality.
Note: Even though typical recorded music is limited in precision to a maximum of 32bits, it is still beneficial to use higher precision for the upsampling process. This is because:
- The upsampling process involves multiple calculations and the use of higher precision helps to reduce the accumulation of errors and maintain the accuracy of the reconstructed signal.
- During the upsampling process, the intermediate samples that are added can have a much higher precision than the original samples and are critical to the perceived quality of the reconstructed signal.
Evaluating Reconstruction Accuracy
In order to evaluate the reconstruction accuracy of an upsampling algorithm, we need to compare the upsampled signal with the original signal sampled at the same rate as the upsampled signal. It is easier to do this comparison with simulated signals as we do not have access to recorded music signals at different rates in a controlled setting. For the purpose of demonstration, we can use band-limited signals that are generated at a lower rate (1fS: 44.1kHz) and upsampled to a higher rate. The upsampled signal can then be compared with the same band-limited signal generated at a higher rate (16dfS: 705.6kHz) to evaluate the accuracy of the upsampling algorithm.
For the purpose of this demonstration, we chose a Band-Limited 44Hz Saw-Tooth (BLST) signal generated at 44.1kHz and
upsampled it to 705.6kHz using various algorithms including PGGB. We chose BLST as it is harmonic rich with
harmonics stopping just short of the Nyquist frequency (22.05kHz), it also has very steep rising edge and a slow decay.
Below is the time domain and frequency response of BLST signal we used.
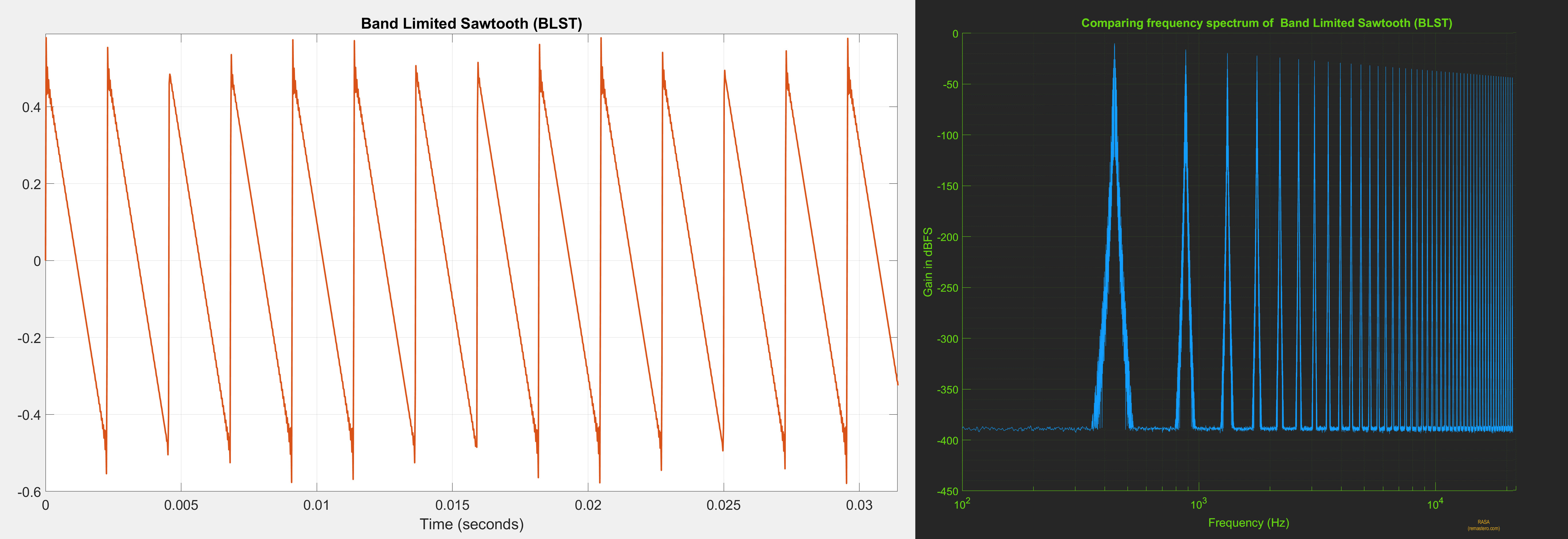
Note: BLST is a stationary, periodic signal and unlike much more complex music signals. It is a good test signal to objectively establish the base line for reconstruction accuracy. If an upsampling algorithm cannot accurately reconstruct BLST, it is even less likely to accurately reconstruct more complex signals.
Comparing Algorithms
Using the 44.1kHz sawtooth signal as input we can now compare the reconstruction accuracy of upsampling algorithms at different precisions. We will look at time domain plots, frequency spectrum of the upsampled signals and also spectrum of the error (i.e., the difference between the reference signal and upsampled signal).
For perfect reconstruction, the upsampled signal should be identical to the reference signal both in time and frequency domain. The error spectrum should be flat and close to the quantization noise floor.
PGGB
PGGB is non-apodizing, with a near ideal transition band and very high attenuation. It uses all the information in the signal and is designed to provide near ideal reconstruction of the original signal. Below are the results of upsampling the BLST signal to 705.6kHz using PGGB at 107 bit precision. The time domain and frequency spectrum of the upsampled signal are shown below.
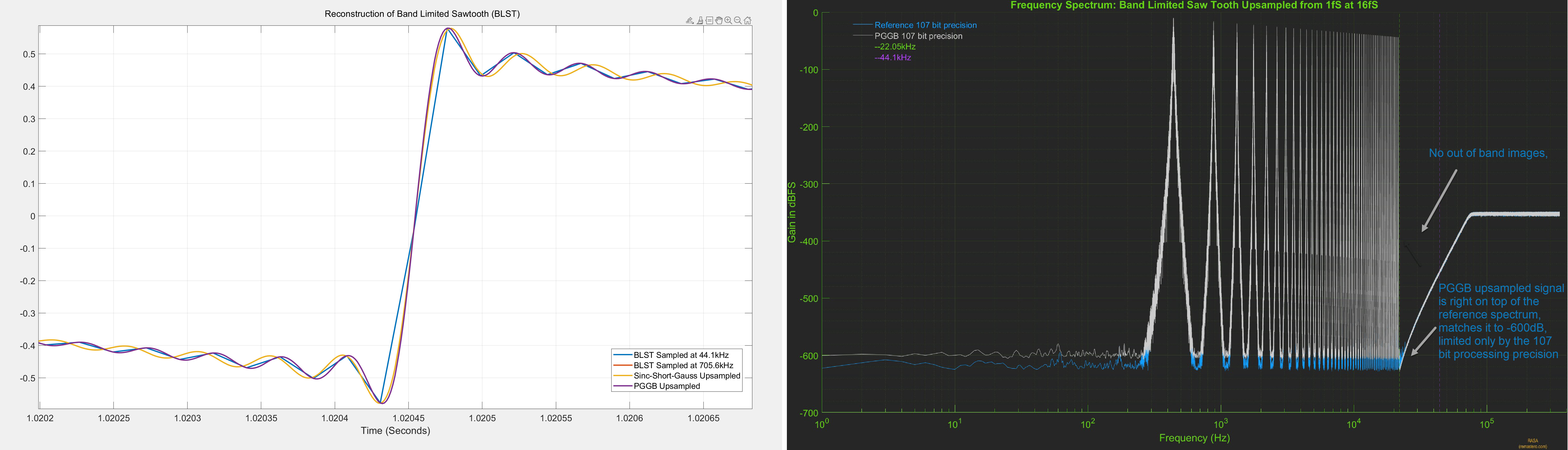 The reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The PGGB upsampled signal (purple) is right on
top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum
of the PGGB upsampled signal (grey) and the reference signal (blue). Here too, PGGB is right on top of the reference
signal and matches it up to -600dB!. We see the same behavior for all precisions (64 bits to 256 bits), irrespective of
the precision used, the PGGB upsampled signal matches the reference signal, limited only by the noise floor of the precision used.
The reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The PGGB upsampled signal (purple) is right on
top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum
of the PGGB upsampled signal (grey) and the reference signal (blue). Here too, PGGB is right on top of the reference
signal and matches it up to -600dB!. We see the same behavior for all precisions (64 bits to 256 bits), irrespective of
the precision used, the PGGB upsampled signal matches the reference signal, limited only by the noise floor of the precision used.
Because the PGGB upsampled signal is right on top of the reference signal both in time and frequency domain, it is hard to tell if there is any difference. It is easier to illustrate reconstruction accuracy by plotting the spectrum of error between the reference signal and PGGB upsampled signal. Below is the plot of the spectrum of the error at all precisions. It clearly shows there are no errors in-band (which includes the audible range). There are no out of band errors either, because all the high frequency images are fully attenuated. What is seen is close to a flat line corresponding to the quantization noise floor for the precision used.
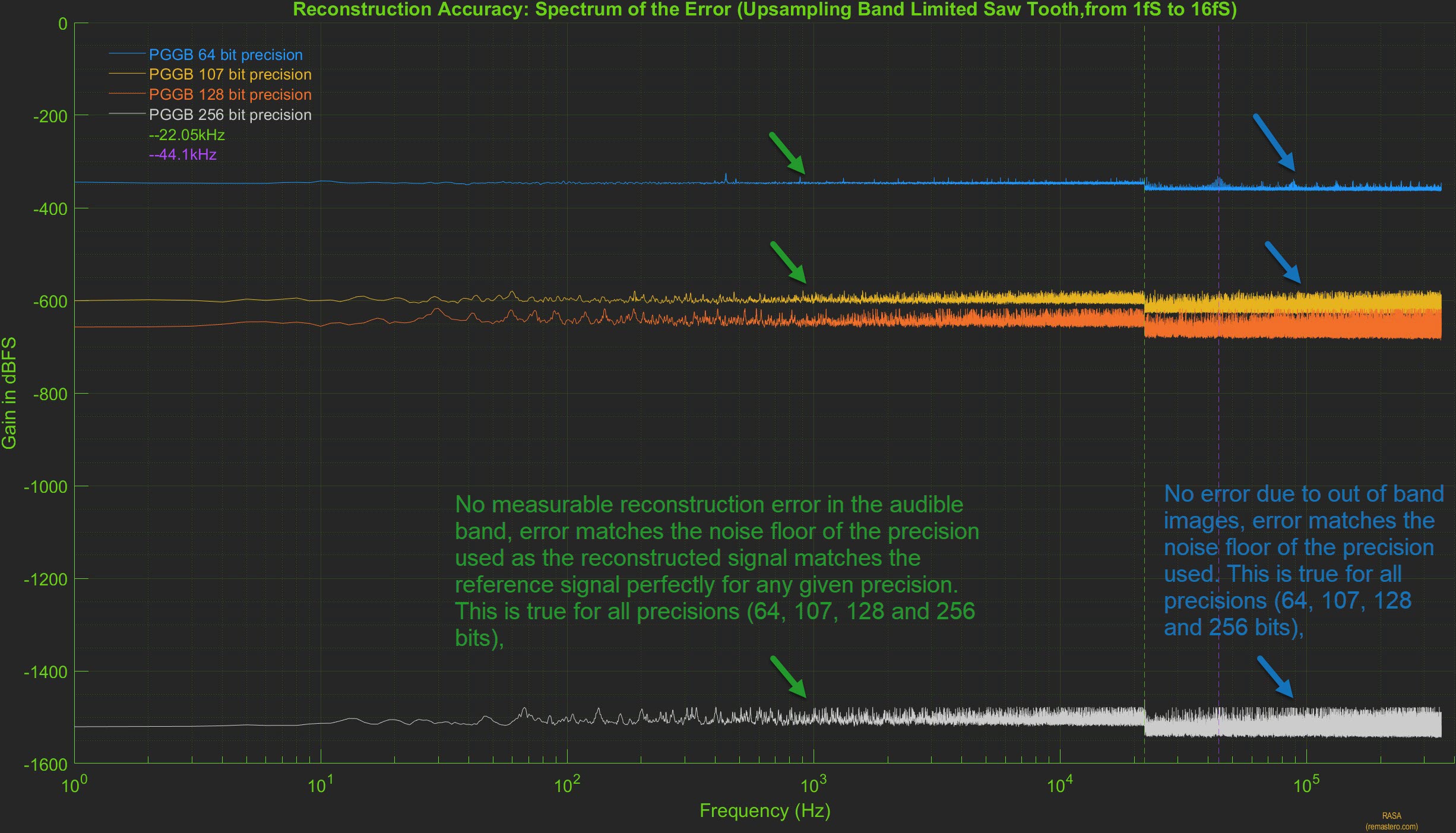
Form the above plots, we clearly see that in the case of PGGB, the reconstruction accuracy is limited only by the quantization noise floor. This is where Noise Shaping plays a big role. If a simple 24 bit or 32 bit dither were to be used, then the reconstruction accuracy will be limited to -200dB or higher and using higher precision would be counter productive.
Short Apodizing Filter (4k Gaussian Windowed Sinc)
Short apodizing filters are designed to have a short impulse response and roll-off close to or slightly earlier than 20kHz with the intent to remove any aliasing artifacts already present in the signal. For this analysis, we chose a linear phase sinc filter with 4065 taps and a corner frequency of 20.5kHz, and used an Approximate Confined Gaussian window (ACGW) with alpha = 0.065. Below are the results of upsampling the BLST signal to 705.6kHz using the short apodizing filter using 107 bit precision. The time domain response of the upsampled signal are shown below.
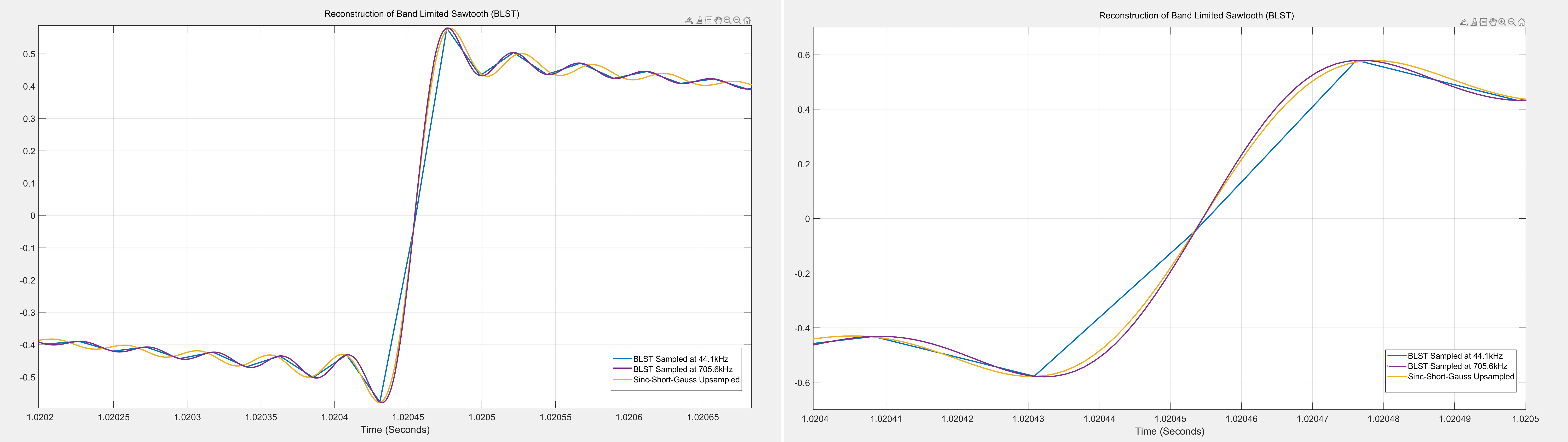 The reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The short apodizing filter upsampled signal
(yellow) does not match reference signal (purple) and is clearly distinguishable. The plot on the right is further
zoomed to show the rising edge and it is very clear that the upsampled signal (yellow) is slower (with a slightly less
steep slope) compared to the reference signal (purple). This behavior should not be surprising given the apodizing
nature of the filter attenuates the higher order harmonics present in the signal. This attenuation will be further
evident in the frequency spectrum of the upsampled signal
The reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The short apodizing filter upsampled signal
(yellow) does not match reference signal (purple) and is clearly distinguishable. The plot on the right is further
zoomed to show the rising edge and it is very clear that the upsampled signal (yellow) is slower (with a slightly less
steep slope) compared to the reference signal (purple). This behavior should not be surprising given the apodizing
nature of the filter attenuates the higher order harmonics present in the signal. This attenuation will be further
evident in the frequency spectrum of the upsampled signal
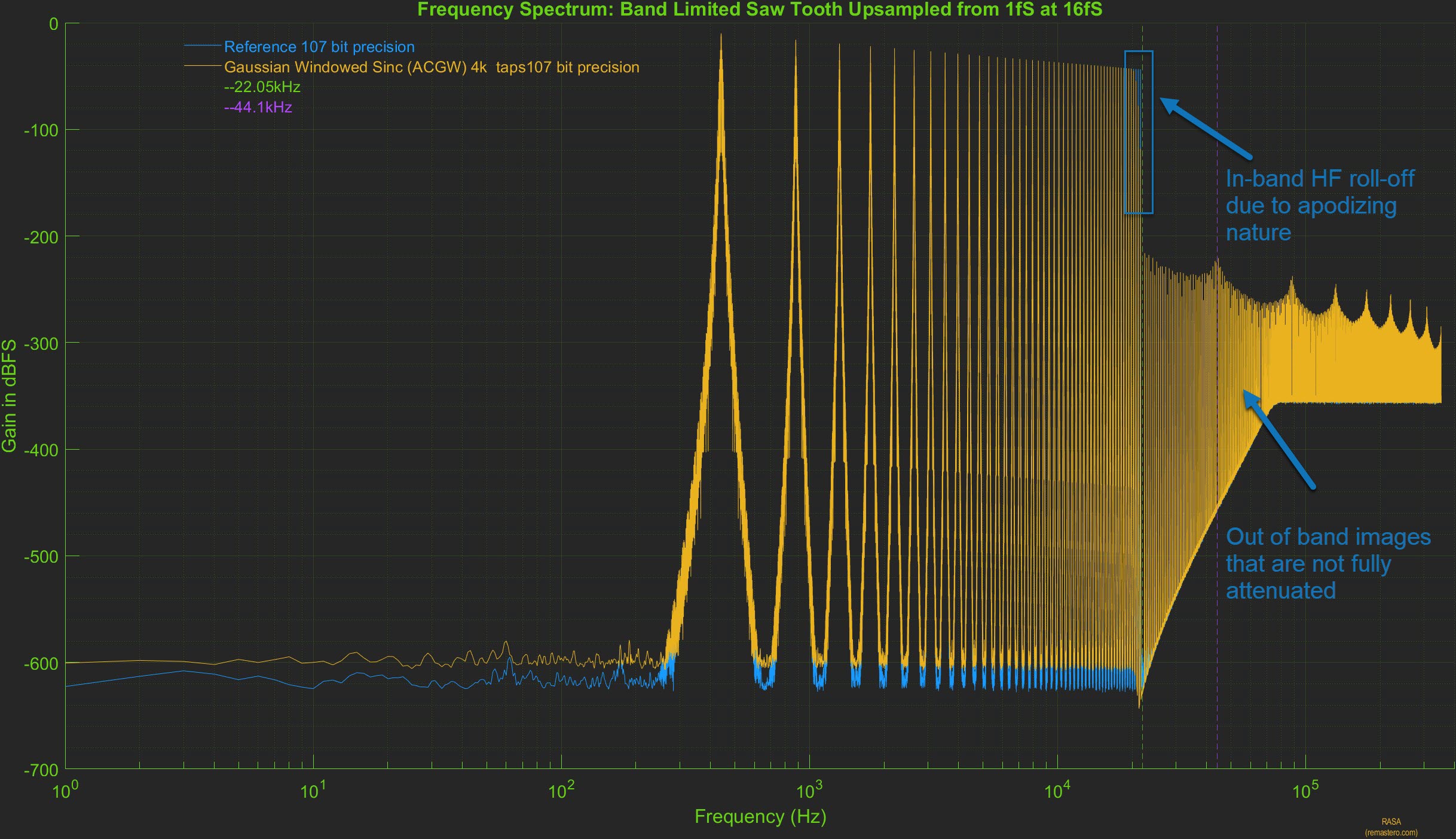 In the plot above, the frequency spectrum of the upsampled signal using the short apodizing filter (yellow) is shown.
Compared to the spectrum of the reference signal (blue), the in-band high frequency roll off can be seen starting close
to 20khz, thus attenuating the higher harmonics present in the original signal. The out of band high
frequency images are not fully attenuated either and this too is evident after the Nyquist frequency of 22.05kHz.
However, in the audible range, it is very hard to tell them apart as the spectrum of the upsampled signal is right on
top of the reference signal.
In the plot above, the frequency spectrum of the upsampled signal using the short apodizing filter (yellow) is shown.
Compared to the spectrum of the reference signal (blue), the in-band high frequency roll off can be seen starting close
to 20khz, thus attenuating the higher harmonics present in the original signal. The out of band high
frequency images are not fully attenuated either and this too is evident after the Nyquist frequency of 22.05kHz.
However, in the audible range, it is very hard to tell them apart as the spectrum of the upsampled signal is right on
top of the reference signal. Here too, it is easier to evaluate the reconstruction accuracy by plotting the spectrum of error between the reference signal and short apodizing filter upsampled signal. Below is the plot of the spectrum of the error at all precisions (on the left). It clearly shows there are three types of error present. Error in the audible range, error due to high frequency roll-off due to apodizing nature of the filter and error in the out of band range as the HF images are not fully attenuated. These errors are due to a combination of factors such as the length of the filter, the window used and the corner frequency of the apodizing filter.
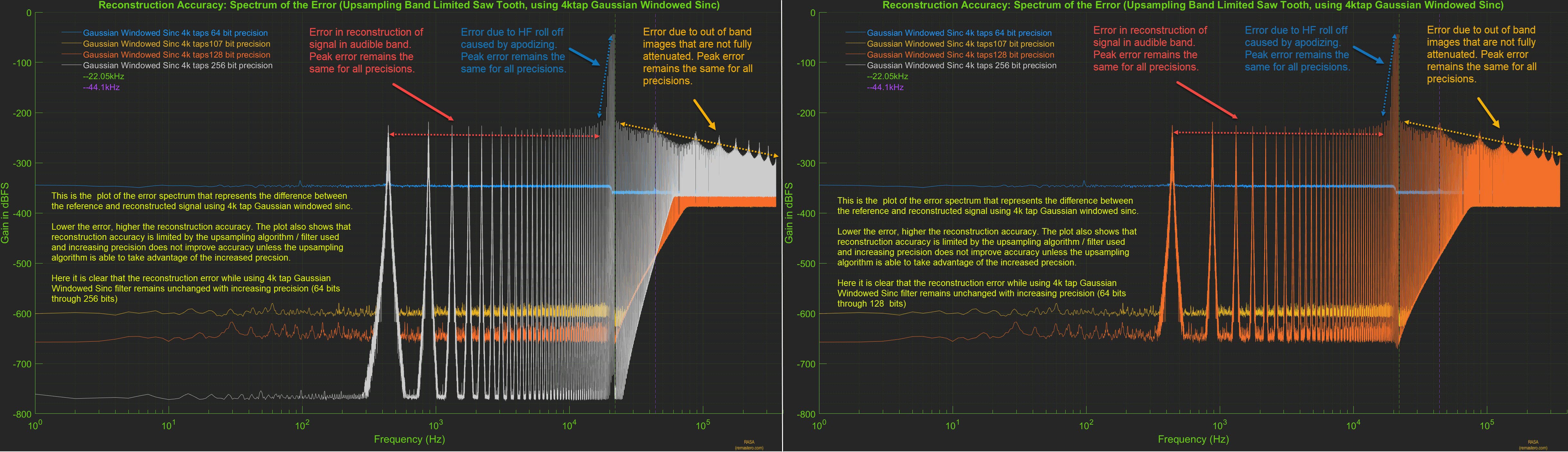
From the above plots, we clearly see that in the case of short apodizing filter, the reconstruction accuracy is limited by the filter design. The reconstruction error remains unchanged with precision, increasing precision reduces the quantization noise floor but the peak error remains unchanged. In the plot on the right, we have removed the error spectrum for 256 bit precision to reveal the error at 128 bit precision. When the upsampling algorithm used is not accurate, it is counter productive to increase the precision and 64 bit precision would suffice for this filter.
Objectively, it is easy to see that this is a far-cry from the near ideal reconstruction seen with PGGB. next, let us see if some of these issues can be remedied by using a long sinc based filter that is non-apodizing
Long Non-Apodizing Filter (2M Flat-top Windowed Sinc)
For this next analysis, we chose a long linear phase sinc filter with 2 million taps, it is non apodizing with a corner frequency that matches the Nyquist frequency of 22.05khz, and used the HFT248D Flat Top window that provides 248db of side lobe attenuation. We chose this filter to illustrate 1. if increasing the number of sinc coefficients can improve the reconstruction accuracy, 2. if the combination of longer filter and the flat top window provides better suppression of out of band HF images and 3. to avoid any intentional attenuation of in band high frequency signals.Below are the results of upsampling the BLST signal to 705.6kHz using the long non-apodizing filter using 107 bit precision. The time domain and frequency spectrum of the upsampled signal are shown below.
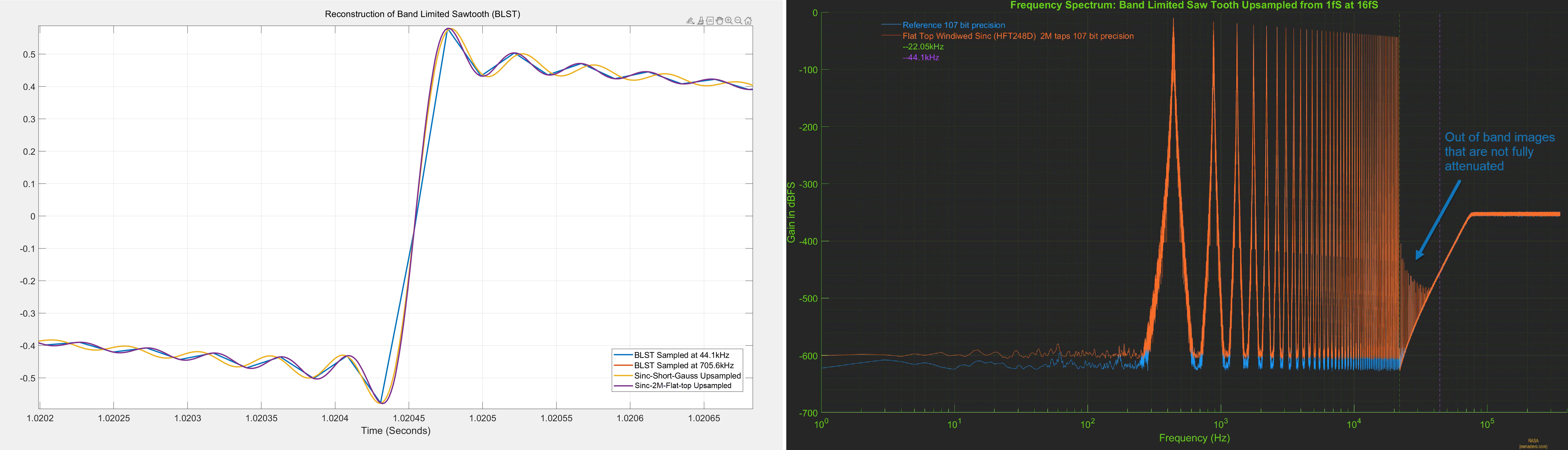 As before, the reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The 2M Sinc upsampled signal (purple) is right on
top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum
of the 2M sinc upsampled signal (orange) and the reference signal (blue). Here the spectrum of 2M sinc upsampled signal
is right on top of the reference signal until the Nyquist frequency of 22.05khz, but unlike PGGB upsampling, we still
see out of band images that are not fully attenuated.
As before, the reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The 2M Sinc upsampled signal (purple) is right on
top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum
of the 2M sinc upsampled signal (orange) and the reference signal (blue). Here the spectrum of 2M sinc upsampled signal
is right on top of the reference signal until the Nyquist frequency of 22.05khz, but unlike PGGB upsampling, we still
see out of band images that are not fully attenuated.
We further evaluate the reconstruction accuracy of the 2M sinc filter by plotting the spectrum of error between the reference signal and 2M sinc filter upsampled signal. Below is the plot of the spectrum of the error at all precisions. It clearly shows there are two types of error present. Error in the audible range, error in the out of band range as the HF images are not fully attenuated. While the longer filter and the flat-top window helped in decreasing both in-band and out of of band errors, it is not near perfect as we saw with PGGB upsampling.
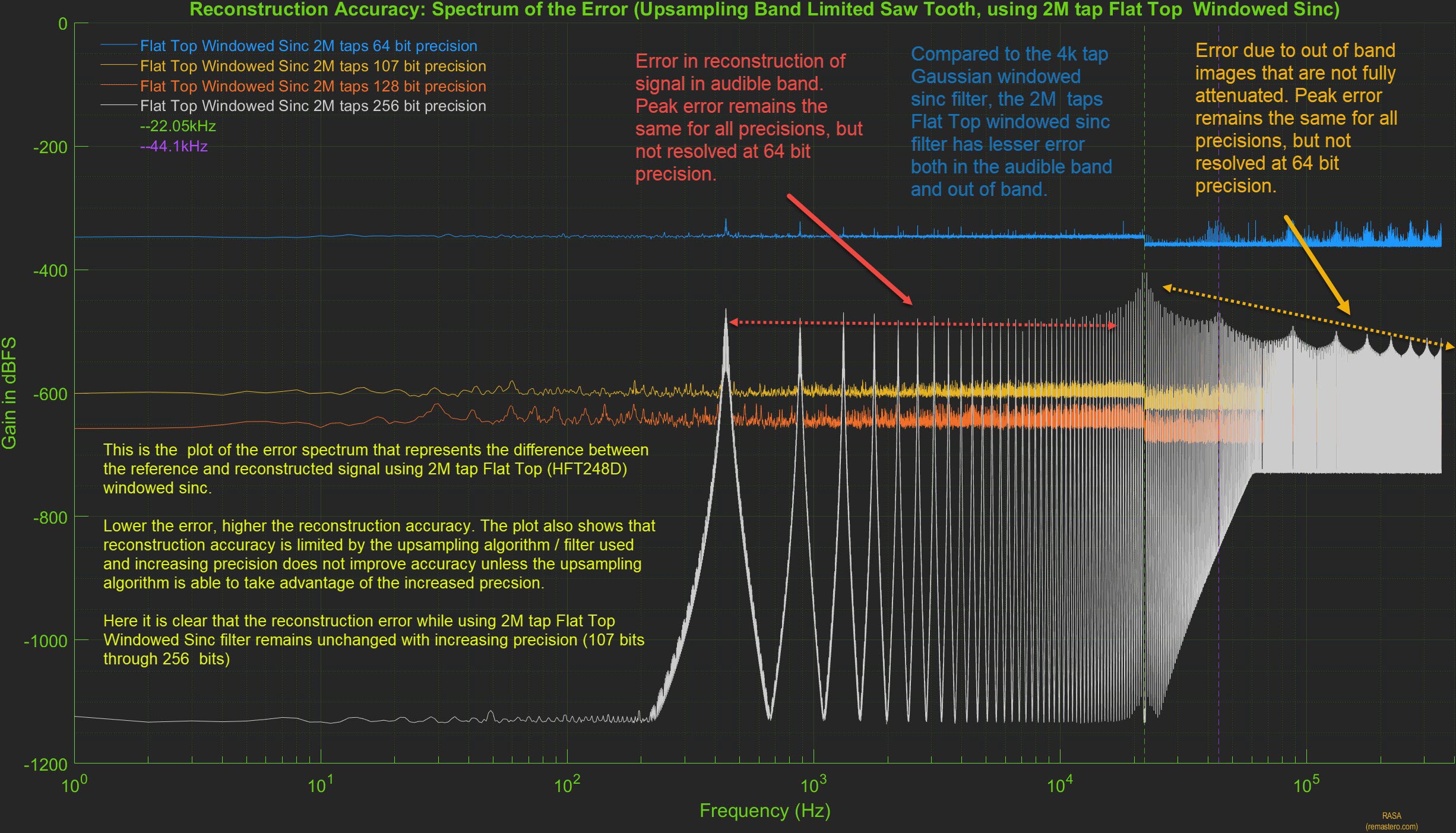
From the above plot, we clearly see that the reconstruction error remains unchanged with precision, increasing precision reduces the quantization noise floor but the peak error remains unchanged. In the case of the 2M sinc filter, it will be counter prodctive to use precisions higher than 75 - 80 bits.
Medium Non-Apodizing Optimized Filter (250k Optimized Windowed Sinc)
We showed previously that even though the long sinc filter with 2M taps did not provide near ideal reconstruction accuracy, it improved significantly over the shorter Gaussian filter. Though the longer sinc filter provided better reconstruction accuracy and better attenuation of out of band images, the filter was not designed with reconstruction accuracy in mind. One can do a lot better with even a shorter filter if the filter can retain more of the original sinc coefficients and at the same time, the window tapper is optimized to achieve better attenuation of out of band images. In fact, this was the approach in the windowed sinc functions used by earlier versions of PGGb (V3 and older). For this analysis, we chose a linear phase, medium length (250k tap) sinc filter, it is non apodizing with a corner frequency that matches the Nyquist frequency of 22.05khz, and we use our proprietary optimized window. We chose this filter to illustrate that a medium length filter can easily improve over a much longer filter if properly designed. Below are the results of upsampling the BLST signal to 705.6kHz using the medium non-apodizing filter using 107 bit precision. The time domain and frequency spectrum of the upsampled signal are shown below.
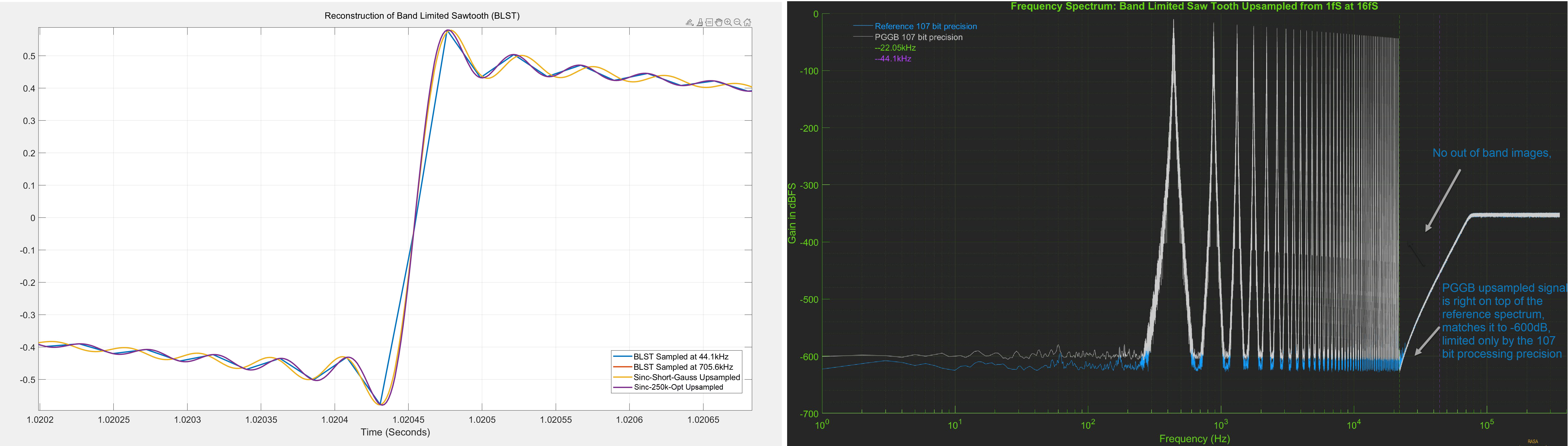 As before, the reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the
time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The 250k Sinc upsampled signal (purple) is
right on
top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum
of the 250k optimized sinc upsampled signal (grey) and the reference signal (blue). Here the spectrum of 250k sinc upsampled
signal
is right on top of the reference signal until the Nyquist frequency of 22.05khz, but unlike the longer 2M sinc filter, we
do not see any out of band images, they are not fully attenuated up to the noise floor of 107 bit precision.
As before, the reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the
time
domain plot, zoomed into one of the rising edges of the sawtooth signal. The 250k Sinc upsampled signal (purple) is
right on
top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum
of the 250k optimized sinc upsampled signal (grey) and the reference signal (blue). Here the spectrum of 250k sinc upsampled
signal
is right on top of the reference signal until the Nyquist frequency of 22.05khz, but unlike the longer 2M sinc filter, we
do not see any out of band images, they are not fully attenuated up to the noise floor of 107 bit precision.
We further evaluate the reconstruction accuracy of the 250k optimized sinc filter by plotting the spectrum of error between the reference signal and 250k optimized sinc filter upsampled signal. Below is the plot of the spectrum of the error at all precisions. We do not see any errors at 64 bit, 107 bit and 128 bit precision, but we see some error near the Nyquist frequency at 256 bit precision we also see that at 256bit, the noise floor is higher than what we saw for PGGB upsampling.
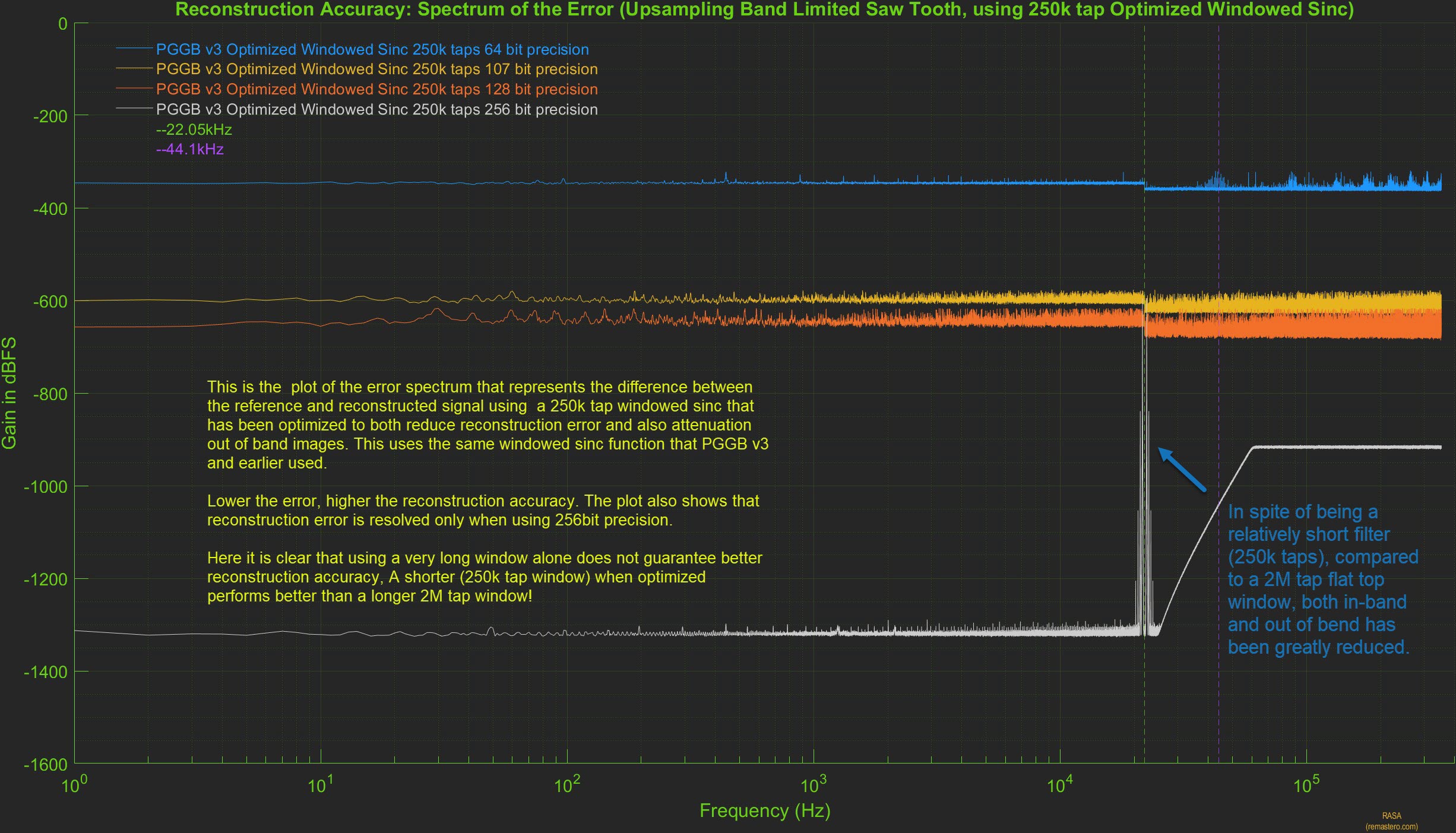 This shows that when properly designed with reconstruction accuracy in mind, a medium length filter can provide much
better reconstruction accuracy, but it may still fall short of the near ideal reconstruction accuracy provided by PGGB
which does not use a windowed sinc function.
This shows that when properly designed with reconstruction accuracy in mind, a medium length filter can provide much
better reconstruction accuracy, but it may still fall short of the near ideal reconstruction accuracy provided by PGGB
which does not use a windowed sinc function.
The Takeaway
We showed that reconstruction accuracy is affected by the type of upsampling algorithm used and that in-band reconstruction error exists even for a relatively simple periodic signal such as the sawtooth waveform. Increasing precision only helps if the upsampling algorithm is accurate and if noise shaping can be used. The PGGB upsampling algorithm provides near ideal reconstruction accuracy, limited only by the quantization noise floor for the precision used.
Myths and Half Truths about Upsampling
Don't test outside of spec!
Many of these myths arise because of either lack of full understanding of sampling theory or misinterpreting it. First, it is important to understand a reconstruction or upsampling algorithm cannot be analyzed by just passing an impulse (pop transient) or a step response. Impulse and step signals have their use, i.e., to understand the frequency and time domain response of a system, but they are not the best way to test a reconstruction/upsampling algorithm. In fact, they are the worst signals you could use to do such a test. It is like testing an equipment outside it's operating range and expecting good results! Sampling theory only guarantees perfect reconstruction when the signal is perfectly band-limited. We understand this is the ideal case and no signal is perfect, so what would be a better test signal? Choose your pick:
- Pure impulse or step: Impulse or step signals are not band limited and have infinite bandwidth and are the polar opposite of what is guaranteed to work.
- impulse or step that is band-limited: Impulse or step that are band-limited, need not be perfect, they should have passed through a low pass filter similar to what ADC would do. Granted, they will still have some aliasing and ringing, but at least it is a test signal that is closer to what a music signal is and also does not totally disregard the conditions for prefect reconstruction. Even if the low pass filter is not a great one, it is still infinitely better test signal.
One example of incorrect testing of resampling algorithms is creating Dirac pulses (pop transients) at high rate (say 352.8k), convert those to 44.1k using the algorithm under test, and finally convert those back to the original rate (352.8k). Dirac pulses do not exist in recorded music signals. Mic pop or clip may be, but they have to pass through the ADC first, which will band limit such pops or transients. Digital reconstruction is about reconstructing the original signal from sampled analog signals that are band-limited, a dirac pulse has no place in such a test as it is of a purely digital origin. The right test would have been to use a filter similar to the ones typically used in an ADC to convert the Dirac pulses from the high rate to 44.1kHz. Then use that signal as an input for testing the reconstruction algorithms.
Bottom line: If an upsampling algorithm is developed based on using non-band-limited signals to test its accuracy (which violates the very basic requirement for reconstruction), it would be calibrated quite differently. It is the equivalent of using English units on a system designed with metric units in mind.
Three wrong reasons
Here are some common misconceptions associated with resampling the PGGB way (i.e., Non-apodizing, using all the information, narrow transition band with high attenuation).
Wrong reason 1: Rings like a bell (maybe for a bat)
It is often claimed that the steep and narrow low pass behavior of PGGB in the frequency domain will result in audible ringing in the time domain. This is simply not true, there will be no ringing if the signal is band-limited (i.e. if it only contains frequencies that are less than half the sample rate). No signal is perfect, if the music was recorded and already went through an ADC, then it is already band-limited as it cannot contain any frequencies above half the sample rate. For CDs, the only content in music that can trigger ringing is one exactly at 22.05kHz where there is very little present because the ADC already attenuated it. The exception is clipped music during post processing, but here too, any ringing one can observe will be exactly at 22.05kHz for CD rates, way beyond normal human hearing (more on audibility).
The whole idea of ringing is way exaggerated (because PGGB's corner frequency is exactly at half the sampling rate). Any ringing one may see will be at 22.05kHz because of the residual energy at the corner frequency left by the ADC, this will not be any more (in peak level) than what you may find with relatively short filters. Any ringing that is already present because of the ADCs filter is left untouched by PGGB and this too is beyond the audible range.
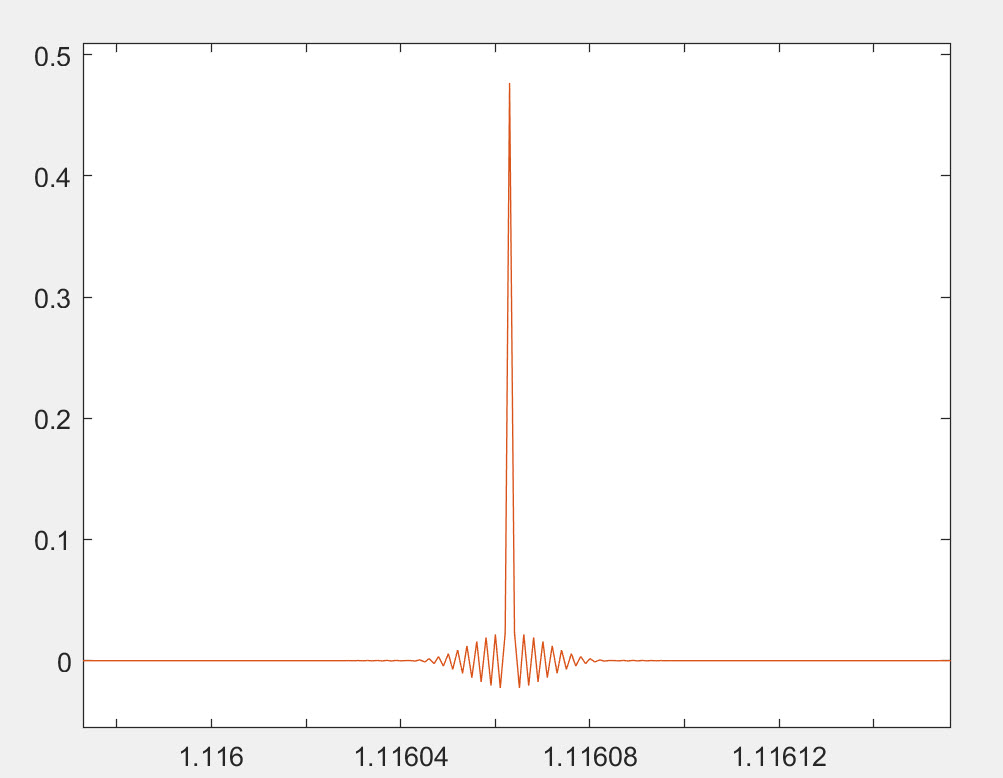
It is easy to demonstrate this with a simple example. We created a 44.1kHz impulse train with multiple, closely spaced Dirac ('pop') transients like the one below.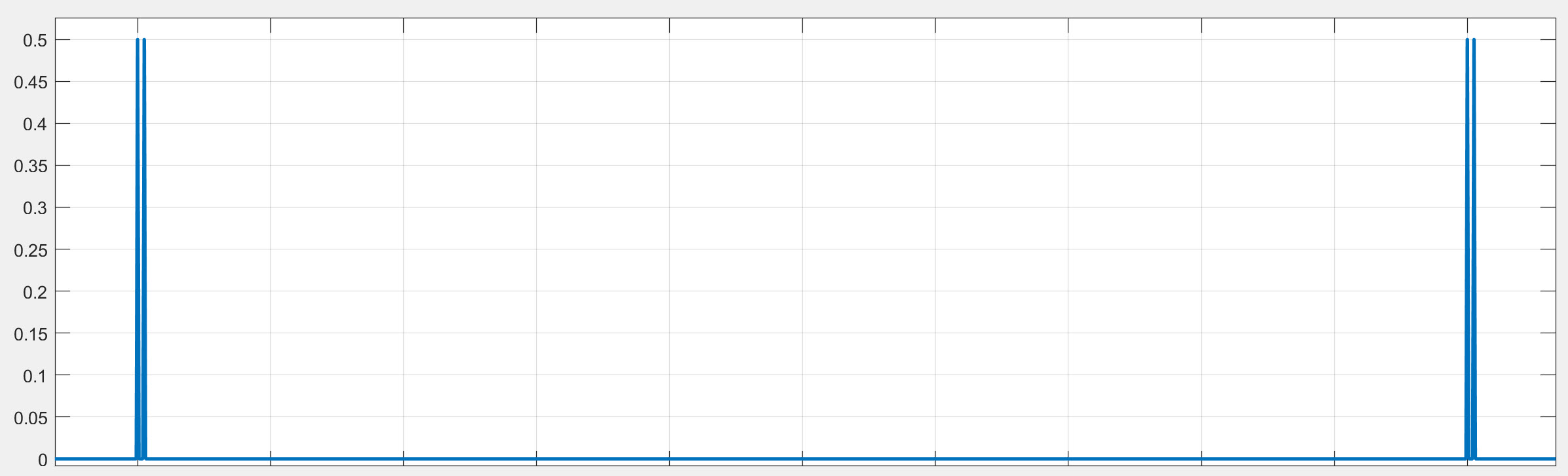 Then to make this an acceptable test signal, we passed it through an IIR filter with a corner frequency at 21kHz
to make it band-limited and create a 44.1kHz test file. This is not a perfect band-limited signal, but it is a much better test signal. You can see the band-limited impulse signal below. You will see it
is not perfect, but it still retains the two transients, and as expected it shows the time domain response of the ADC
filter. It is not an infinite band-width signal anymore.
Then to make this an acceptable test signal, we passed it through an IIR filter with a corner frequency at 21kHz
to make it band-limited and create a 44.1kHz test file. This is not a perfect band-limited signal, but it is a much better test signal. You can see the band-limited impulse signal below. You will see it
is not perfect, but it still retains the two transients, and as expected it shows the time domain response of the ADC
filter. It is not an infinite band-width signal anymore.
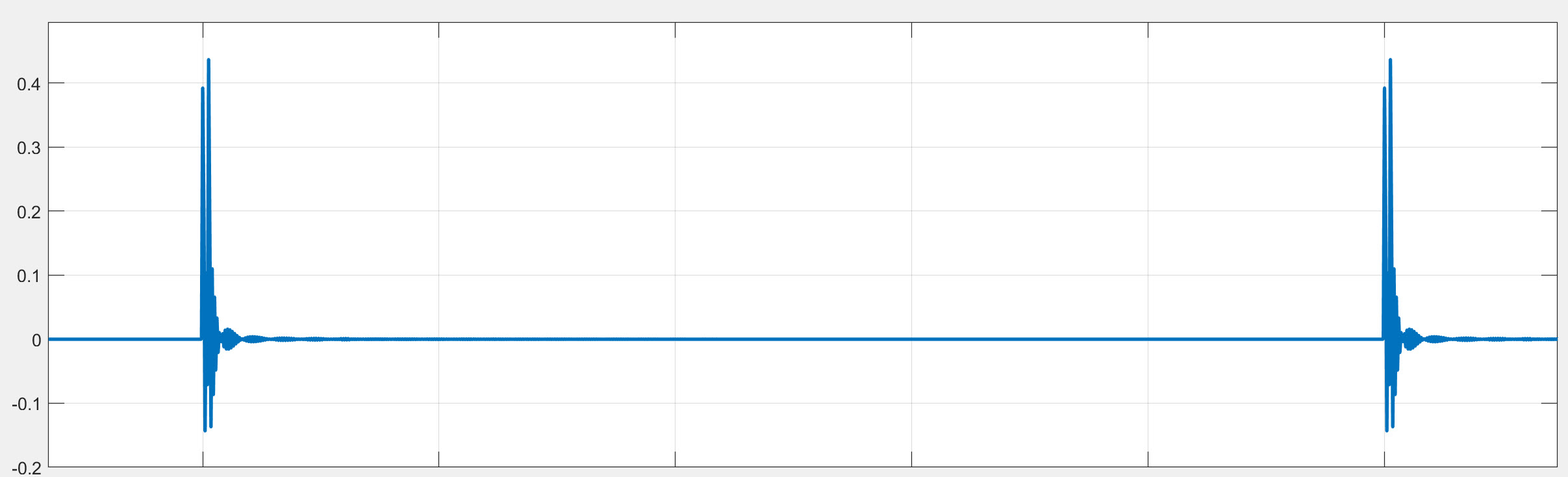 We then used PGGB to upsample it
16x using default settings and 128bit precision and created a 705.6kHz upsampled file. We then used a short linear phase Gaussian
apodising filter to upsample to the same 705.6kHz. The Gaussian filter we used is a short Gaussian polyphase sinc filter, the Gaussian filter's time domain response is provided below.
We then used PGGB to upsample it
16x using default settings and 128bit precision and created a 705.6kHz upsampled file. We then used a short linear phase Gaussian
apodising filter to upsample to the same 705.6kHz. The Gaussian filter we used is a short Gaussian polyphase sinc filter, the Gaussian filter's time domain response is provided below.
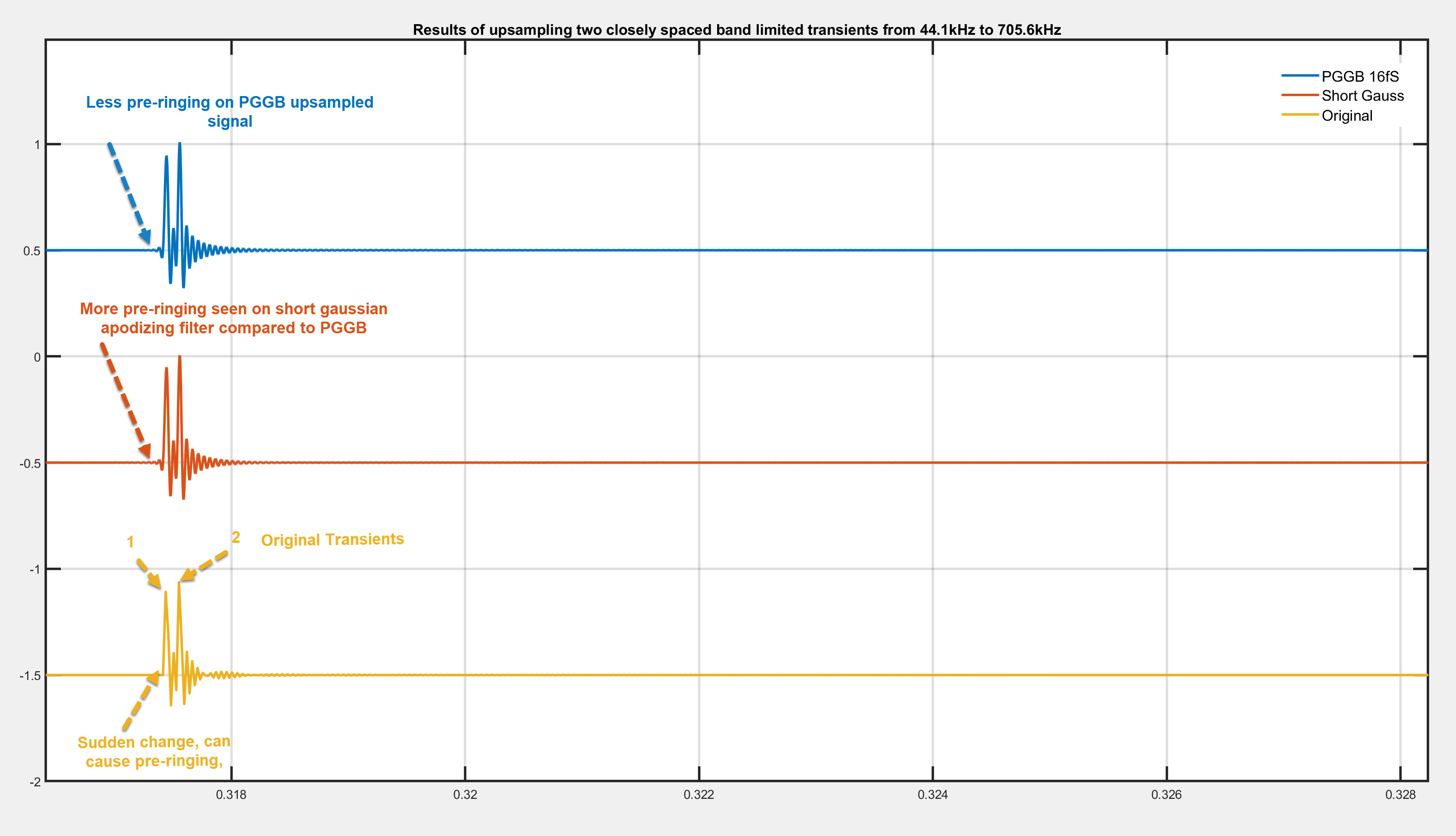
 Below we show the results (you can click on the image to make it bigger). Blue (PGGB), Red (Short Gauss) and
Yellow is the original. We only zoomed in on one set of transients, but the same is true with all of the transients. You will notice that:
Below we show the results (you can click on the image to make it bigger). Blue (PGGB), Red (Short Gauss) and
Yellow is the original. We only zoomed in on one set of transients, but the same is true with all of the transients. You will notice that:
- You can make out the two transients clearly in all three signals
- There is some pre-ringing in the PGGB upsampled signal, this is expected because the band-limiting filter is not perfect, but you can see very little. Which again is beyond the audible range to cause any change in perception of the transient.
- Ironically, there is pre-ringing even in the short Gauss upsampled signal and this is more than what you see with PGGB. To be fair, you will not hear this either.
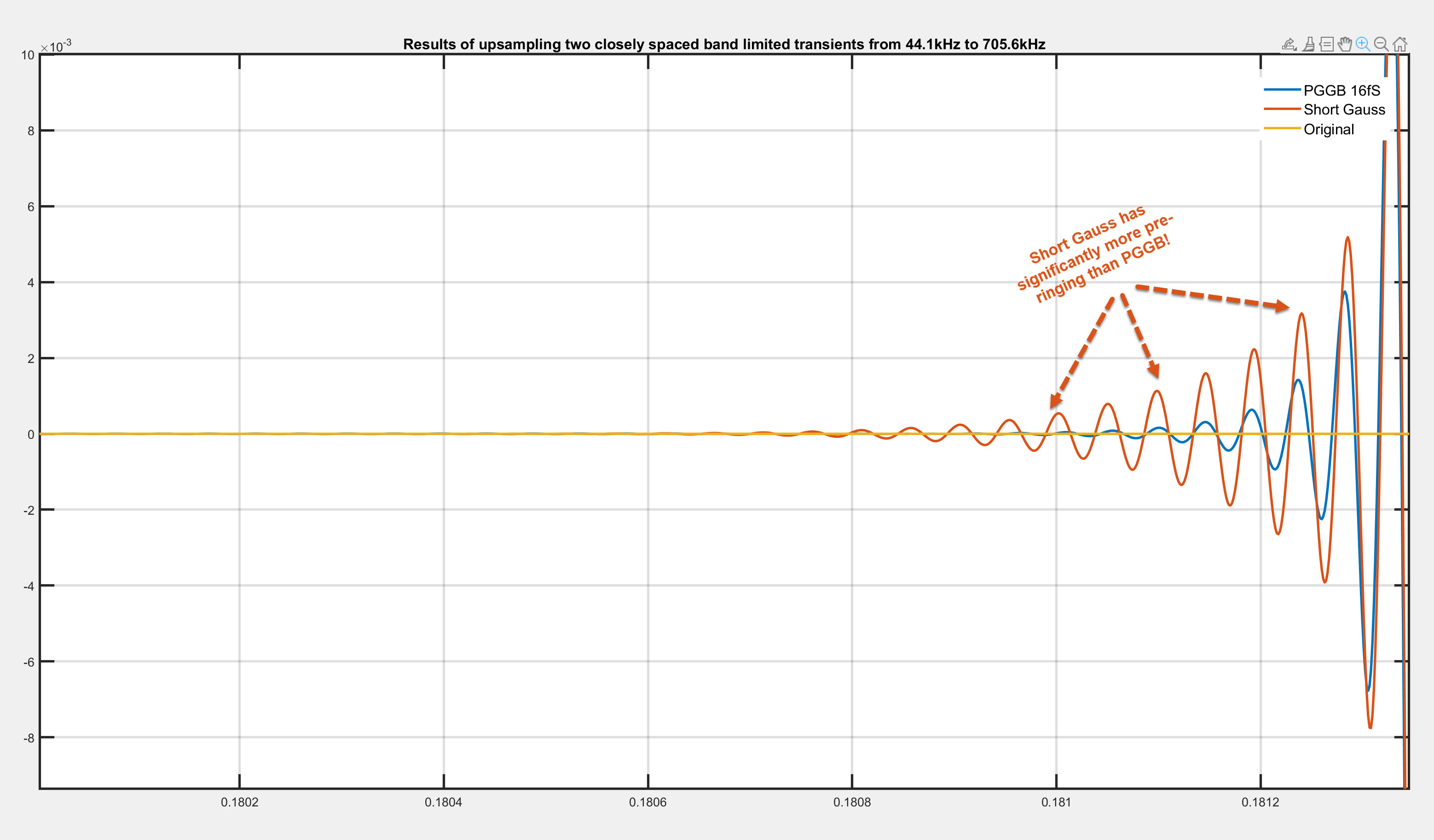
 We zoom in on the pre-ringing portion of the first transient to show the time domain response of the three
signals. Here you can clearly see the pre-ringing in the short gauss signal is more than the PGGB signal
We zoom in on the pre-ringing portion of the first transient to show the time domain response of the three
signals. Here you can clearly see the pre-ringing in the short gauss signal is more than the PGGB signal
 Now let us repeat the above test with a real track. For this test we chose a 44.1kHz track that has a lot
of clean transients and also contains clipping. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Pérez And John Patitucci and was downloaded from Qobuz. We upsampled this track to 705.6kHz
using PGGB and short Gaussian polyphase sinc filter, the same as the one we used above. We set the gain to -1.5dB to
prevent limiting or clipping and then scaled it back by +1.5dB so we can compare the signals. We also used Gaussian
dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
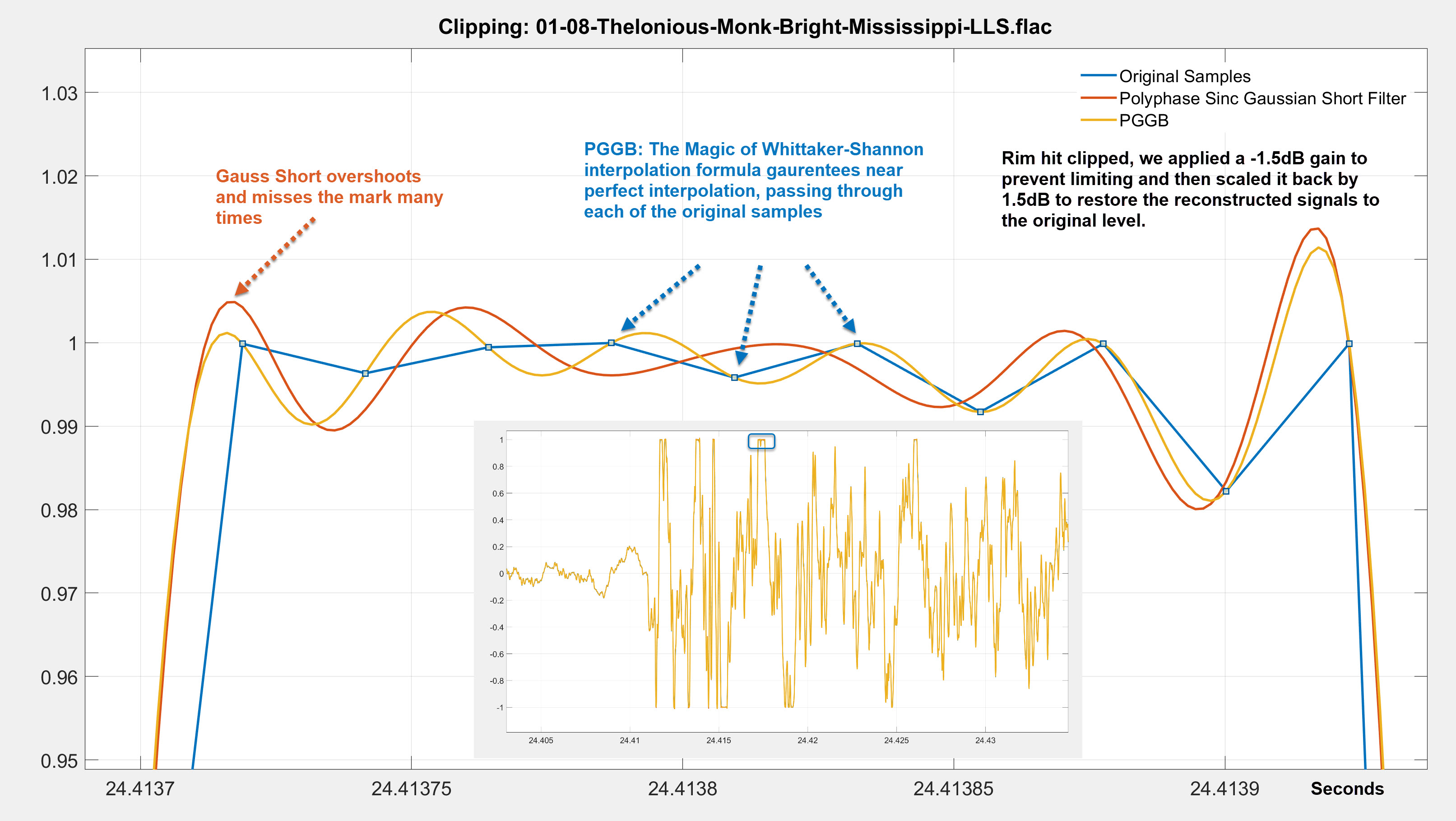
We zoom in on a section where there was a rim hit and the track clipped. Below we show the results (you can click on the image to make it bigger). Blue (Original), Red (Short Gauss) and
Yellow is the PGGB.You can see that:
Now let us repeat the above test with a real track. For this test we chose a 44.1kHz track that has a lot
of clean transients and also contains clipping. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Pérez And John Patitucci and was downloaded from Qobuz. We upsampled this track to 705.6kHz
using PGGB and short Gaussian polyphase sinc filter, the same as the one we used above. We set the gain to -1.5dB to
prevent limiting or clipping and then scaled it back by +1.5dB so we can compare the signals. We also used Gaussian
dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
We zoom in on a section where there was a rim hit and the track clipped. Below we show the results (you can click on the image to make it bigger). Blue (Original), Red (Short Gauss) and
Yellow is the PGGB.You can see that:
- PGGB does a near perfect job of reconstruction, passing through each of the original samples even when they clipped.
- The short Gaussian filter both undershoots and overshoots compared to PGGB, this very similar to what we demonstrated previously regarding pre-ringing.
- It is very easy to see that PGGB does better even when the signal clipped, because the signal has been band-limited already.
The only time significant ringing can be shown is when it is either an artificial signal (such as an impulse, step) with no band-limiting or if post processing causes clipping. Even if clipping is present this ringing is at half the sample rate which for CD is 22.05kHz, which is beyond the human hearing range, it does not affect signals in the audible range, and is barely noticeable!
So, if someone listens to a whole lot of artificial signals instead of music, or a lot of clipped music, and they have an extended hearing range beyond 20kHz, we can understand their concern. But for the rest of us, it is a non-issue.Wrong reason 2: Blurs transients (show us your math)
It is claimed that long linear filters will cause transient blurring because they are using information both from the future and the past to reconstruct transients and hence both future and past samples could potentially affect a transient that is being reconstructed presently. First, PGGB does not use such filters, so this argument is moot. But even if it did, the argument is pure conjecture without a mathematical basis. If this were true then the whole sampling theorem would fall apart because it is built on the premise of being able to use infinitely long sinc based linear filters to perfectly reconstruct band-limited sampled signals. Anyone claiming so should support their argument with a mathematical proof.
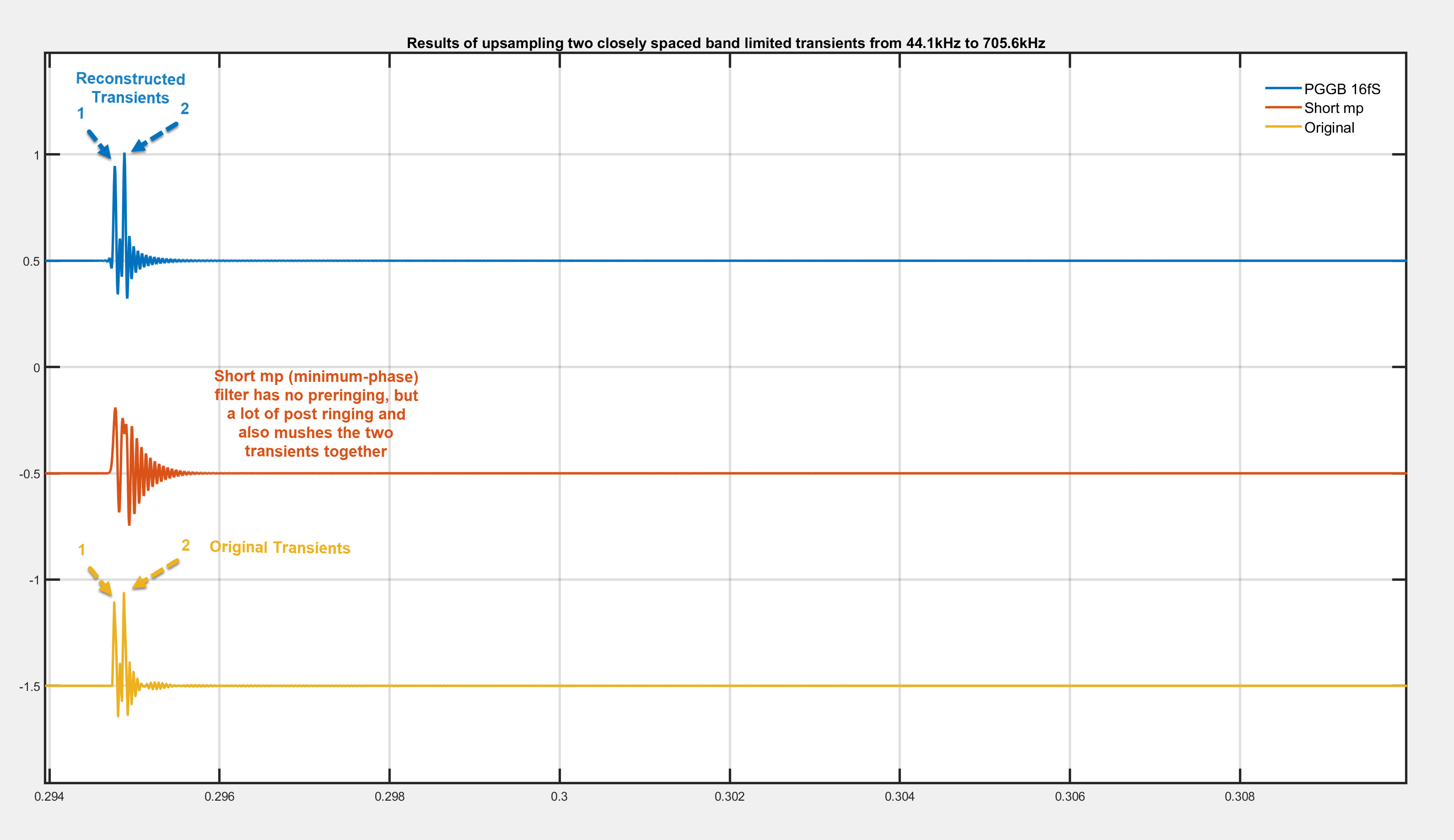
It is fairly simple to demonstrate this with real music tracks, but we chose the more dramatic example of band-limited impulses we used previously. We then used PGGB to upsample band-limited, closely spaced Dirac pulses (pop transients) at 44.1kHz to 705.6kHz using default settings and 128bit precision. We also used a short minimum phase filter which is recommended by some as an ideal filter for music containing strong transients such as pop and rock. minimum phase version of short polyphase sinc filter, the filter's time domain response is provided below.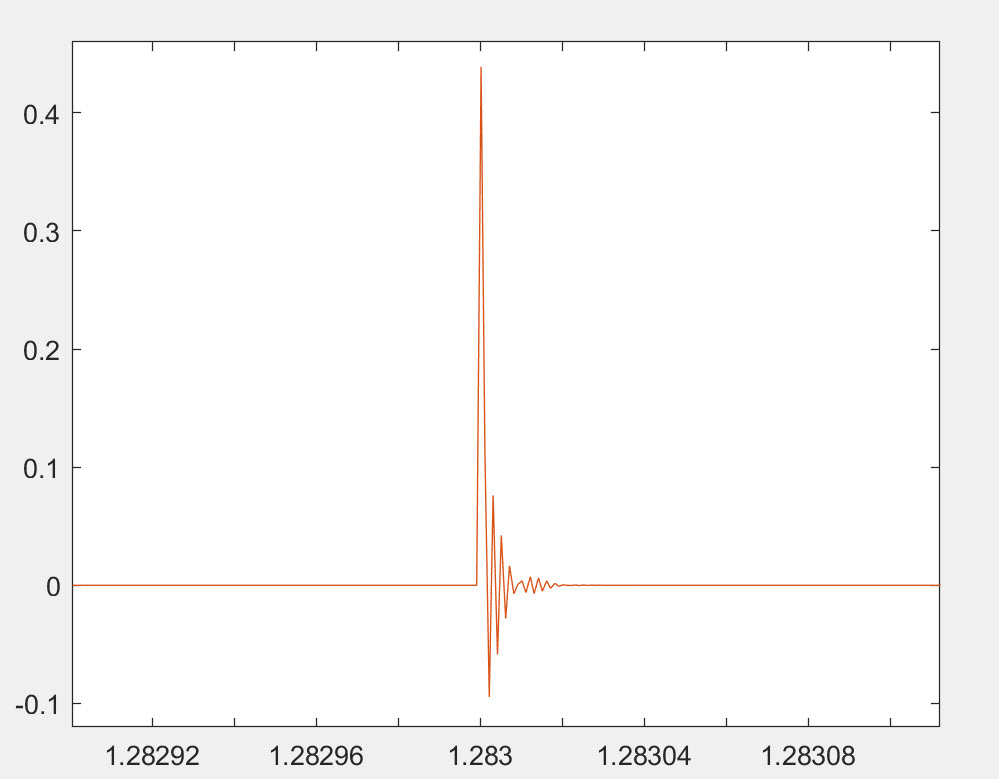 Below we show the results (you can click on the image to make it bigger). Blue (PGGB), Red (short mp) and
Yellow is the original. We only zoomed in on one set of transients, but the same is true with all of the transients. You will notice that:
Below we show the results (you can click on the image to make it bigger). Blue (PGGB), Red (short mp) and
Yellow is the original. We only zoomed in on one set of transients, but the same is true with all of the transients. You will notice that:
- You can make out the two transients clearly in the original signal and the one upsampled by PGGB
- The short mp filter which is recommended for music with transients ironically is the one that blurs the transients!
- The only saving grace for short mp filter is that there is no pre-ringing (which is beyond the audible range anyway, but it comes at the huge cost of post ringing and blurred transients!
 Now let us repeat the above test with a real track. For this test we chose a 44.1kHz track that has a lot
of clean transients, the same one as before. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Pérez And John Patitucci and was downloaded from Qobuz. We upsampled this track to 705.6kHz
using PGGB and minimum phase version of short polyphase sinc filter, the same as the one we used above. We also used Gaussian
dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
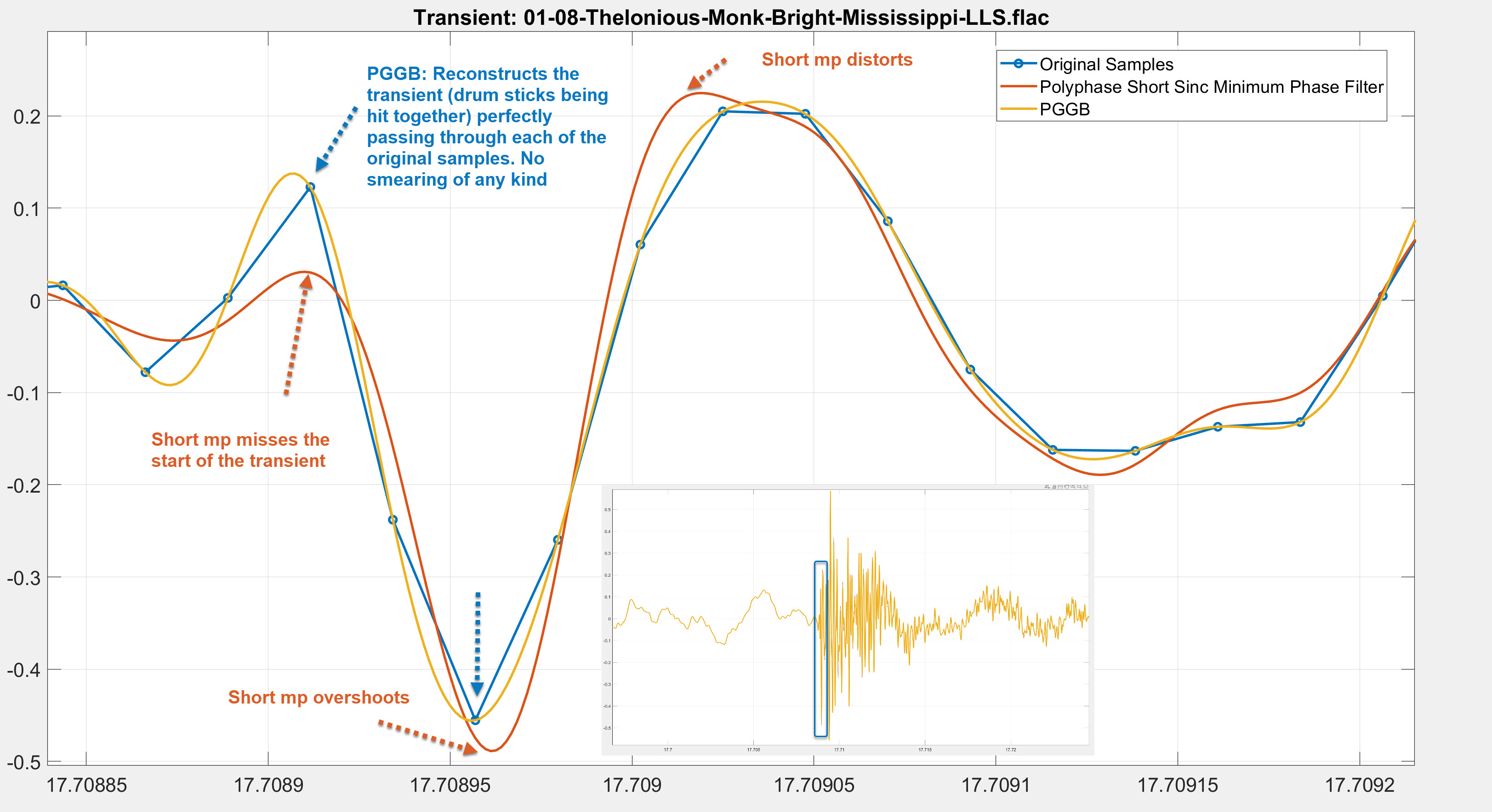
We zoom in on a section where there was a clean transient when two drum sticks were hit together. The results are shown
below (you can click on the image to make it bigger). Blue (Original), Red (Short mp) and
Yellow is the PGGB. You can see that:
Now let us repeat the above test with a real track. For this test we chose a 44.1kHz track that has a lot
of clean transients, the same one as before. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Pérez And John Patitucci and was downloaded from Qobuz. We upsampled this track to 705.6kHz
using PGGB and minimum phase version of short polyphase sinc filter, the same as the one we used above. We also used Gaussian
dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
We zoom in on a section where there was a clean transient when two drum sticks were hit together. The results are shown
below (you can click on the image to make it bigger). Blue (Original), Red (Short mp) and
Yellow is the PGGB. You can see that:
- PGGB does a perfect job of reconstruction of the transient, passing through each of the original samples.
- The short mp filter misses the start of that transient, overshoots and distorts.
- It is very easy to see that PGGB does a perfect job of reconstructing transients, there is no blurring.
Wrong reason 3: Oversampling filters affect outcome only above audible band (why so naive?)
It is sometimes argued that ringing that is outside of human audible range, can have audible effects on the in-band music. The reasoning given is that, if this were not true, all oversampling filters and all DAC's internal upsampling should sound the same, because they only affect the out-of-band signal. This is a rather naive argument that focuses only on the frequency domain! it assumes these filters do not affect the time domain transients, transient reconstruction and reconstruction of small signals. All these filters sound different not because we are super human and suddenly hear above 20kHz. While evaluating DACs or digital oversampling filters, it is important to focus on time domain cues such as depth, layering, resolution and transient quality, not tonality. Because every change we make to the reconstruction algorithms affect how the transients are reconstructed in the time domain and in turn, affects our perception of transients and the construction of the virtual soundscape.
This too is very easy to illustrate with the very same example that we used previously. We compare the original band-limited signal (yellow) with the PGGB upsampled signal (Blue) and the short mp upsampled signal (Red).- You can clearly see how the transients are reconstructed differently by PGGB and short mp filter
- The short mp filter which is recommended for music with transients blurs the transients, while PGGB preserves them just fine.
- PGGB will sound different from short mp filter not because of any pre-ringing that is beyond the audible range, but because it is more faithful to the original transients. However short mp that blurs transients will sound flat lacking depth (which may be fine for some music like Rock). The blurring of transients that can lump the energy in to 'clumps' could give the perception of stronger transients, and it is a smoother and more forgiving sound. For that reason it could still be good for music such as rock and pop.
 Now let us repeat the above test with a real track using the same one as before. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Pérez And John Patitucci downloaded from Qobuz. We upsampled this track to 705.6kHz
using PGGB and minimum phase version of short polyphase sinc filter, the same as the one we used above. We also used Gaussian
dither for both PGGB and the short minimum phase filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
We zoom in on a section where there was a clean transient when two drum sticks were hit together. The results are shown
below (you can click on the image to make it bigger). Blue (Original), Red (Short mp) and
Yellow is the PGGB. You can see that:
Now let us repeat the above test with a real track using the same one as before. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Pérez And John Patitucci downloaded from Qobuz. We upsampled this track to 705.6kHz
using PGGB and minimum phase version of short polyphase sinc filter, the same as the one we used above. We also used Gaussian
dither for both PGGB and the short minimum phase filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
We zoom in on a section where there was a clean transient when two drum sticks were hit together. The results are shown
below (you can click on the image to make it bigger). Blue (Original), Red (Short mp) and
Yellow is the PGGB. You can see that:
- PGGB does a perfect job of reconstruction of the transient, passing through each of the original samples.
- The short minimum phase filter misses the mark many times, overshoots and also distorts.
- PGGB clearly demonstrates better reconstruction accuracy here. The obvious change in shape of the reconstructed waveforms will have an audible effect.
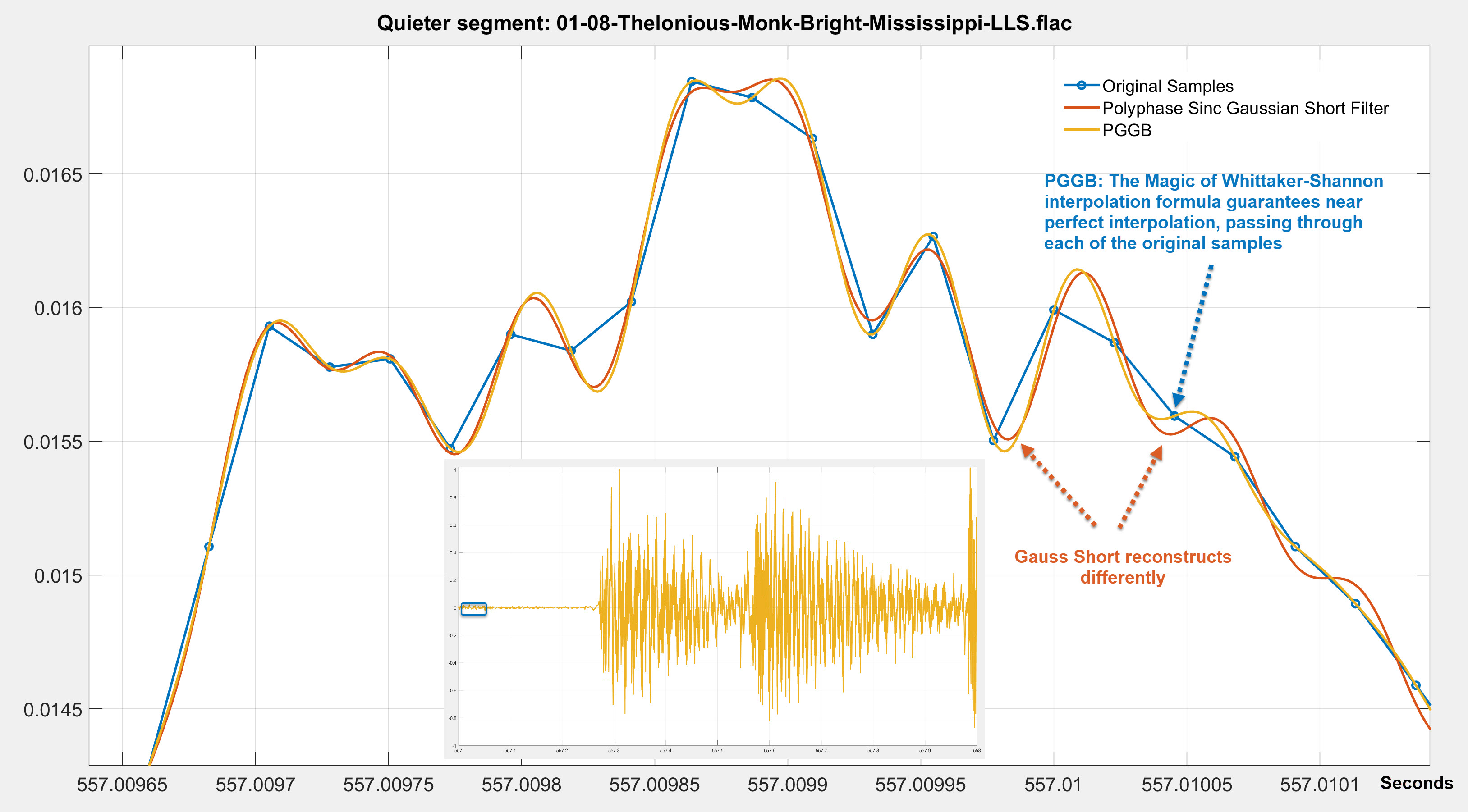
 As another example, we use the same track again, but we chose a relatively quiet part of the track and we upsampled this track to 705.6kHz
using PGGB and short Gaussian polyphase sinc filter. We also used Gaussian
dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
Below we show the results (you can click on the image to make it bigger). Blue (Original), Red (Short Gauss) and
Yellow is the PGGB.You can see that:
As another example, we use the same track again, but we chose a relatively quiet part of the track and we upsampled this track to 705.6kHz
using PGGB and short Gaussian polyphase sinc filter. We also used Gaussian
dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track.
Below we show the results (you can click on the image to make it bigger). Blue (Original), Red (Short Gauss) and
Yellow is the PGGB.You can see that:
- The Magic of Whittaker-Shannon interpolation formula guarantees near perfect interpolation, passing through each of the original samples even for this relatively low level signal.
- The short Gauss filter reconstructs differently in comparison which is easily observable in time domain, but the differences are small.
- It is very easy to see that PGGB reconstructs low level signals differently, and why they could be audibly different be it transients or low level detail.
Let us show you how oversampling filters affect outcome in the audible band too!
One way to illustrate how oversampling filters can affect the outcome in the audible band is by plotting the difference between the same audio track that was upsampled with two different oversampling filters in both time domain and in the frequency spectrum. But there are a few challenges in accomplishing this:- The first challenge is it is very hard to align the two upsampled signals perfectly at a sample level to do the comparison. Depending on the upsampling algorithm used, they could introduce a sub-sample shift that would make the differences look much larger than they truly are. The solution is not to try and align the signals by correcting for the sub-sample shift. This is because, any processing can alter the signals we are trying to compare and invalidate the comparison. Since PGGB does not introduce a sub-sample shift, the only way to do this comparison is to choose a filter that does not introduce a sub-sample shift, so we chose the sinc based halfband filter.
- The second challenge is that though we can relatively easily plot the differences in time domain, it is harder to show the differences in the frequency spectrum using FFTs. This is because, subtle yet audible differences in the audible range get averaged out.
Did we pretend Gibbs phenomenon did not exist and defy physics?
Please do not jump to any such conclusions. If you are wondering Gaussian filters have the most compact time-frequency footprint, then how is it plausible that PGGB has less peak ringing than a short Gaussian filter? As far as the plots go, what you see is what you get, so it is mathematically possible. The answer lies in the corner frequency. The Gaussian filter we used is a short Gaussian polyphase sinc filter (it is not a minimum phase filter), the Gaussian filter's time domain response is provided below. The Gaussian filter is linear, and apodizing and has a corner frequency earlier than the Nyquist, while PGGB has a corner exactly at 22.05kHz.
Any ringing you see in
time domain is the result of the filter having to dissipate the energy beyond its cutoff frequency. So as the filter's
cutoff frequency increases, the ringing will become more localized in time (i.e., will also increase in frequency)
because it only needs to dissipate the energy that exceeds the cutoff frequency, everything else just passes through. So PGGB will ring exactly at 22.05kHz for CD rates and every other frequency just passes through.
The Gaussian filter is linear, and apodizing and has a corner frequency earlier than the Nyquist, while PGGB has a corner exactly at 22.05kHz.
Any ringing you see in
time domain is the result of the filter having to dissipate the energy beyond its cutoff frequency. So as the filter's
cutoff frequency increases, the ringing will become more localized in time (i.e., will also increase in frequency)
because it only needs to dissipate the energy that exceeds the cutoff frequency, everything else just passes through. So PGGB will ring exactly at 22.05kHz for CD rates and every other frequency just passes through.An apodising filter has to deal with all the leftover energy starting from its cutoff frequency till the Nyquist that was left unfiltered by the ADC which will be more than what PGGB has to filter. While PGGB has to deal with whatever little energy that is left at the Nyquist after the ADC has already done what it can. So, it is not entirely surprising that you see less ringing with PGGB on a reasonably band-limited signal. Here by 'less' we mean the peak magnitude of pre-ringing (after all, the peak magnitude prior to a transient is likely to affect transient perception, if it is even audible!). Ultimately this is all about law of conservation of energy. A short filter has to dissipate the residual energy past its corner frequency within its time domain footprint, the shorter it is, the more it has to dissipate within the short duration. So this is a function of both the length of the filter and its corner frequency. The peak pre-ringing for PGGB can be less, though the duration can be longer, with a lower magnitude. So we did not cheat Gibbs, and again this is all beyond the audible range.
Of course, the less performant the ADC filter is and you push the corner frequency of the ADC filter further out you will see more ringing with PGGB till the ADC's filter becomes a Dirac pulse and the signal is not band-limited any more. What these examples illustrate is that testing with Dirac pulses and making blanket statements about ringing and their audibility shows a fundamental lack of understanding of sampling theory.
There is so much misinformation about what is the correct way to test a resampling algorithm, we perfectly understand if you do not trust us. Feel free to repeat these experiments with the band limited test file we used: Band-limited 44.1kHz impulse train and check for yourself using your preferred upsamplers.
TLDR: While a close-to-ideal reconstruction algorithm such as one used by PGGB may cause ringing beyond the audible range, a non-ideal filter, be it short or long, will affect the whole audible band with poor transient reconstruction and can be audible.
It looks like PGGB can process really fast in 64 bit precision, can it do this on streamed music?
There is a real-time version available for Foobar2000 as a plugin. This version is limited to 64bit precision.
PGGB is available in a SDK form for OEM, for that exact purpose. SDKs are available for Windows, Mac and Arch Linux.
The SDK is in the form of C++ header file and static libraries.
Developing a player from scratch that will both play local files and streaming audio is a huge undertaking, and also
doing it the right way (managing buffers, load balancing and keeping any processing noise to an absolute minimum etc.)
is even harder.
One option We considered is for PGGB to sit in between an existing player and an endpoint or like a plugin. The
problem with this approach is the latency will be unacceptable as PGGB in the middle will only have access to the stream
at the rate at which the host application sends the data. For this reason, the only way I would implement PGGB in real
time is if I had direct access to the full track or multiple tracks (this is possible even for streamed data as most
players will cache the tracks in advance).
The PGGB in SDK form uses a different framework for performance and is light weight and our tests indicate after just a
few seconds of startup delay, gap-less playback is possible.
Are linear phase filters better for upsampling?
Upsampling requires a low pass filter
( to interpolate
intermediate samples). The purpose of the filter
is to provide good estimates of the intermediate samples so that the upsampled
signal is smooth
and as close to what the original music signal would have been.
There are several ways to implement the low pass filter and each method has its pros
and cons. Linear phase filters maintain the phase relationship of the
original signal
and tend to preserve the timing of the original signal, resulting in improved
imaging precision.
Minimum phase filters when compared to linear-phase filters of the same length,
have better frequency domain performance that results in better tonal accuracy and a
denser presentation,
For the above reason, for short lengths, minimum phase have a
significant advantage over linear phase filters. With longer filter lengths, the
choice becomes
more subjective and comes down to preference and synergy with the playback chain.
With, the ultra-long windowed Sinc based linear filters such
as the one PGGB-AP uses, it is possible to get very close
to the original, as if the music was recorded at a higher sample rate. As a result,
the ultra-long filters pull ahead
of other implementations in terms of realism and accuracy.
The ultra-long windowed Sinc based linear filters come with a significant cost in
terms of
latency and computational requirements, which make them hard to use for real-time
playback. However,
for offline upsampling and remastering, they are an excellent choice.
PGGB use a proprietary method different from the above methods. PGGB is non apodizing and it does not use windowed
sinc functions, or long filters either. The best way to look at the current approach used by PGGB is that it considers
the track as a whole. If no HF filters are enabled (which is the default for CD and 2fS rates), PGGB keeps all of the
original samples intact, then creates intermediate samples all at once by time shifting all of the original samples. Our method approaches the theoretical
limit of reconstruction accuracy possible for a track of given length and sample rate. This is
more accurate than using pure Whittaker-Shannon coefficients with windowing. As the sample rate increases, and the track
length increases, our method approaches the mathematical equivalence of using pure sinc based interpolation.
Why use noise shaping? Is it same as dither?
Both dither and noise shaping can be used to
reduce the audible effects of
quantization (i.e., digital noise). Quantization noise is introduced when
the remastered track that resides in memory
in 64-bit floating-point precision format,
but needs to be output at 32-bit integer precision or lower.
However they work in very different
ways.
Dither is the
process of adding an intentional small
random noise to randomize quantization noise. This serves to decorrelate the music
signal and quantization error, resulting
in a more natural sound. Dither does not reduce the quantization noise, it just
helps to mask it.
Noise
shaping
does not simply mask the quantization noise, but it instead pushes the noise out of
the audible range.
Well implemented noise shapers can almost completely eliminate quantization noise
from the audible range.
This helps preserve and reproduce even the smallest of changes accurately, resulting
in a clean
and almost analog like quality. While noise shaping provides better results, unlike
dithering, noise shaping can
only be used if the output sample rate is 8fS (DXD) or higher.
PGGB uses specially designed higher order noise shapers
that are optimized for output sample rates and bit depths and are designed to almost
completely
remove quantization noise from the audible range.
What is a 'HF Noise filter'?
HF noise filter refers to 'High frequency' noise filter.
Most Hi-res recordings (4fS or higher) contain a significant amount of
residual noise (beyond 30kHz) as a result of noise shapers used during analog to
digital
conversion process. There is no music information contained in this noise.
So the HF noise can be safely removed, and has a positive effect on sound quality.
PGGB offer a choice of three HF noise filters. However the HF noise filters
are not applied separately, instead they are integrated into the design of
resampling process.
Just like adding more elements to a camera lense can reduce transparency,
using additional filters can reduce transparency. So PGGB uses a single optimized
process that does both
reconstruction and HF noise filtering for the most transparent sound.
Does PGGB use Apodizing filters?
PGGB does not use apodizing filters.
Apodization in Greek means cutting off the foot. It has different technical meanings
depending on the application. In Signal processing, it just means using a windowing function to reduce ringing artifacts
due to the abrupt truncation at the beginning and end of a sample window. In digital-audio, the term has been used and also misused.
In digital-audio, more often than not 'apodizing' is used to mean it is a non-brick-wall filter which has reduced or no 'pre-ringing'.
It is implemented as a slow-roll off filter.
Will my DAC benefit from PGGB?
- High rate PCM and DSD: DACs that support PCM rates of 705.6/768kHz or higher and DACs that support DSD rates DSD256 or higher will benefit most from PGGB remastered tracks.
- PCM NOS: DACs that do little to no processing (such as R2R DACs that can be run in NOS mode) and DACs whose oversampling filter can be turned off will benefit significantly from PGGB PCM remastered tracks.
- Pure DSD: DSD DACs that have a pure DSD mode that can be enabled will benefit significantly from PGGB PCM remastered tracks.
- On DACs that support up to DXD rates and DSD128, remastering CD quality tracks using PGGB to DXD rate (352.8kHz) and DSD128 is likely to be beneficial too.
- If you have a DAC that supports PCM only, then you can use PGGB to remaster DSD to the highest rate supported by your DAC with excellent results.
- If you have a DAC that supports only 96kHz or 192kHz, you can use PGGB to remaster DSD or DXD files to rates that are supported by your DAC.
Does PGGB support DSD upsampling?
Yes, PGGB currently supports upsampling to DSD or PCM rates.
What is 1fS, 2fS, ..., 32fS etc?
One useful concept to learn is the terminology of FS. This refers to 'Fundamental Sample rate'. 1fS refers to 44.1 or 48 kHz. Thus:
How big are PGGB remastered tracks?
As a rule of thumb, every 11 minute 25 seconds of a stereo track at 16fS and 32 bits or DSD512
takes up about 4GB of space. So, on an average typical CDs that
are 40 - 45 minutes long will take about 16GB of space at 16fS 32 bits/DSD512 file.
At 8fS 32 bits that is 8GB and at 8fS 24 bits it will be 6GB.
Remastered .wav tracks that are bigger than 4GB will be split, but the metadata
is preserved and track numbering
is changed so that they will play sequentially and in a gap-less fashion.
Does PGGB support lossless compression?
PGGB supports FLAC for bit depths less than or equal to 24 bits and
sample rates less than 8fS.
PGGB also supports WavPack compression format for higher than 8fS rates or
bit depth higher than 24 bits. WavPack compression is also lossless like FLAC.
PGGB will transfer all tags and artwork to both FLAC and WavPack output files.
What sort of PC will I need for running PGGB?
PGGB is a resource intensive application. It will benefit from as many CPU cores, as much physical RAM, and fast NVMe
drives you can give it. That said, the application has been tuned extensively to scale to the available resources,
so while a machine with lesser RAM or fewer cores may take longer to process a file, it will not fail, nor will the
processing time grow exponentially.
Recommended system specification:
- At least 4 cores, 8 cores preferred
- 16GB RAM if processing Cds with tracks less than 12 minutes for PCM. For more flexibility, at least 32 GB is recommended, and 64GB or 128GB will reward you even more if your library and DAC call for it and if you wish to upsample to DSD. For detailed memory requirements, see here
- A fast NVMe SSD for input and output files, and paging file
- Recommend at least 128GB paging file for PCM and 512GB for DSD (see guide for details PC, Mac)
- Ideal build (for PCM and DSD)
- Custom Quiet PC (for PCM and some DSD)
- Taiko Audio Extreme (for PCM)
- Quiet PC Serenity 8 Office (quietpc.com, for PCM and some DSD): Nanoxia Deep Silence 1 Anthracite Rev.B Ultimate Low Noise PC ATX Case. ASUS PRIME Z370-A II LGA1151 ATX Motherboard. Intel 9th Gen Core i7 9700K 3.6GHz 8C/8T 95W 12MB Coffee Lake Refresh CPU. Corsair DDR4 Vengeance LPX 64GB (4x16GB) Memory Kit. Scythe Ninja 5 Dual Fan High Performance Quiet CPU Cooler. Gelid GC-3 3.5g Extreme Performance Thermal Compound. Palit GeForce RTX 2070 8GB DUAL Turing Graphics Card. FSP Hyper M 700W Modular Quiet Power Supply. Quiet PC IEC C13 UK Mains Power Cord, 1.8m (Type G). 2 x Samsung 970 EVO 2TB Phoenix M.2 NVMe SSD (3500/2500)
- 2010 Mac Pro running Parallels (PCM): It was able to run PGGB with 6 cores and 32 GB of RAM but currently running 12 cores and 128 GB. Parallels was given at least 4 cores and at least 28 GB.
- For PCM and some DSD: Streacom FC10 Alpha fanless chassis, Asus Prime Z490-A mainboard, Intel i7-10700 LGA1200 2.9 GHz CPU, CORSAIR Vengeance 128GB (4 x 32GB) DDR4 SDRAM 2666, OPTANE H10 256GB SSD M.2 for Windows 10 Pro OS, SAMSUNG 970 EVO Plus SSD 2TB M.2 NVMe with V-NAND Technology, HDPLEX 400W HiFi DC-ATX power supply.
- For PCM: iMac Pro (2017) — 3.2 GHz 8-Core, 32 GB, 1TB, Apple Bootcamp, Windows 10
- For PCM: iMac, 48GB RAM, 3.3 GHz four core i5. Running Windows 10 Pro under Bootcamp with a shared drive set up
- The sample rate of the source track: The higher the rate, the more virtual memory is needed
- The length of the track: The longer the track, the more virtual memory is needed
Can you suggest a sample PC build for PGGB that is also quiet?
Sure we can:
- Be quiet! Pure Base 500, No PSU, ATX, White, Mid Tower Case . Caveat - It’s a nice quiet case, but nothing great to look at.
- Prime B460-Plus, Intel® B460 Chipset, LGA 1200, HDMI, ATX Motherboard
- Core™ i7-10700 8-Core 2.9 - 4.8GHz Turbo, LGA 1200, 65W TDP, Retail Processor
- 128GB Kit (4 x 32GB) HyperX FURY DDR4 2666MHz, CL16, Black, DIMM Memory. Caveat - can easily start with 64GB
- 750 GA, 80 PLUS Gold 750W, ECO Mode, Fully Modular, ATX Power Supply
- Be quiet! Dark Rock 4, 160mm Height, 200W TDP, Copper/Aluminum CPU Cooler
- 2TB 970 EVO Plus 2280, 3500 / 3300 MB/s, V-NAND 3-bit MLC, NVMe, M.2 SSD
Can I use the Taiko Audio Extreme to run PGGB application?
As extreme as the Taiko Extreme is, it is not quite extreme enough out of the box to
run PGGB. The Extreme has a stripped down installation and memory configuration that
is optimized for SQ during playback. PGGB consumes all available system resources
(and then some). The good news is that you can install PGGB on the Taiko Extreme and
run it when you are not listening to music and not impact SQ.
To get PGGB to run on the Extreme, you must configure a paging file when
upsampling. By default, the Extreme has the paging file disabled to maximize sound
quality. To run PGGB, you will be turning on a paging file, running PGGB, then
disabling the paging file and rebooting, then listening to music on your Extreme as
you normally do (for convenience, you can listen to music with the paging file on,
but there may be some SQ impact).
To turn on the paging file on your Extreme, from the Start menu, follow the
following path:
Start -> Windows System -> Control Panel -> System -> Advanced System Settings ->
Advanced -> Performance Settings -> Advanced -> Virtual Memory Change
Select the drive on which you want to put the paging file (C: drive
usually), and select “custom size.” Set to 135000 for both min and max. Click OK and
you’re paging file is ready to go.
When you turn on or increase the size of the paging file, you do not need to reboot.
If you shrink it or disable it, you will need to reboot for the change to take
effect.
Note that the default configuration of the Extreme has the paging file disabled,
because it could impact SQ. For best sound quality, turn on your paging file, run
PGGB, then turn it off and reboot before listening to music.
If you’re doing a lot of PGGB work, give a listen to playback with and
without the paging file to decide if the inconvenience of rebooting your system
prior to music playback is worthwhile for you.
At 48GB, the Taiko Extreme is at the minimum amount of memory that you need to run
PGGB. Typically it does OK, but upsampling DXD files or processing DSD files pushing
the system to its limits. If you’re processing overnight, you won’t notice, but
enjoy a cup a coffee if you’re sitting there waiting for these more intensive
processing jobs to run.
If I had both PCM and DSD versions of an Album, which do I choose to remaster?
Regarding DSD… there are so many factors that come into play: original recording format, original editing and mixing format, your DAC, etc., etc. Ultimately, it all boils down to a couple of key considerations:
- Is the DSD album the best-sounding version in your library? If so, just upsample with PGGB - it will uplift SQ.
- If you also own PCM versions of the album, or are aware of other PCM versions, by all means explore upsampling your best-sounding PCM version with PGGB, and then choose the best-sounding upsampled versions.
Example 1:
Mahler 2nd, Gilbert Kaplan, Vienna Philharmonic, DG hybrid SACD. I don’t know the details of the recording, editing, and mastering format. Played natively to my DAVE in DSD+ mode, the DSD layer sounds best, with the CD layer played in PCM+ mode second best. I upsampled both versions to 32/705.6 with PGGB, played back natively on DAVE in PCM+ mode (of course), and found the following to hold:Example 2:a) the upsampled DSD version still sounds better than the upsample CD version
b) the gap between the 2 versions shrunk. In other words, PGGB did more good to the PCM version, but the improvement to the DSD version was still extraordinary.
Das Lied von der Erde, MTT, SF Symphony, recorded in DSD64, but unclear what format it was edited and mixed in. I suspect it was PCM, but not sure. I own 3 versions: DSD and CD from the hybrid SACD, and 24/96 hi-res version purchased from Qobuz. Played natively on my DAVE, I find the 24/96 (2fS) version to sound best, with the DSD version 2nd best. After upsampling with PGGB:Bottom line in all of this is:a) The upsampled 24/96 version reigns supreme.
b) The gap between the upsampled 24/96 and upsampled DSD is greater than the native gap. This again suggests PGGB’s ability to impart magic is most with PCM, but DSD is also uplifted.
Pick the best sounding version of an album in your library (irrespective of PCM or DSD). Where it’s close or equal, always prefer the PCM version.
Does PGGB support multi-channel music?
PGGB currently does not support multi-channel PCM or DSD, but it is relatively easy to extend it to support multi-channel. If there is modest demand for it, or a requirement for a commercial application,we are open to offering multi-channel support. Just drop us an email.
Do you use Matlab?
PGGB no longer uses Matlab as of version v7. PGGB uses QT for cross platform GUI.
The core of PGGB processing for 64 bit, 128 bit, and 256 bit is written fully in C/C++ and that is why there
is already a real-time option that is free and is available as a Foobar2000 plugin that runs at 64bit precision and does not use Matlab runtime. The PGGB C++ core is cross platform compatible and works on
Windows, Mac and Linux.
We do not intentionally design software that will require a lot of resources (RAM and time), in fact performance optimization
is one of our areas of research. The reason PGGB takes so much resources is because 256bit computations of this nature
take a lot of time. We are confident in saying that we have the fastest and most memory efficient implementation
on the planet (if one considers the equivalence of using a filter that is about the same length as the number of samples in the
track, computed at the output rate, with 256 bit precision). There is no free lunch, if one wants the ultimate quality in reconstruction, there are no shortcuts. We can of course design shorter
filters that are faster and need less memory, but then it will not be PGGB any more, there are alternate options that do
that.
It is very easy to compare speeds by setting 64bit, 128bit and 256bit precision in PGGB and see the difference
in speed. Please be warned, if you are running a trial version processing will stop after 2 tracks at 128bit or higher
precision. So if you run PGGB in trial mode overnight, do not be surprised if you only see 2 processed
tracks in 7 hours! It did not take 7 hours to process, it just stops after three tracks. For example, on a Windows PC
with a 8-core, 3.6GHz i9 CPU and 64GB
RAM, an average CD (44.1kHz) track converted to 16fS rate will be processed at about 1x - 0.8x speed at 256bit
precision. There are both text and csv logs in the output folder that show the actual time taken.